四川省宜宾市2018届九年级数学中考模拟试卷（一）
试卷更新日期：2018-08-10 类型：中考模拟
一、单选题
-
1. 计算（a3）2的结果是（ ）A、a5 B、a6 C、a8 D、a92. 太阳的半径约为696000km，把696000这个数用科学记数法表示为（ ）A、6.96×103 B、69.6×105 C、6.96×105 D、6.96×1063. 已知关于x的一元二次方程x2＋2x－a＝0有两个相等的实数根，则a的值是（ ）A、4 B、－4 C、1 D、－14. 为了考察某种小麦的长势，从中抽取了10株麦苗，测得苗高（单位：cm）为：16 9 14 11 12 10 16 8 17 19，则这组数据的中位数和极差分别是（ ）
A、13，16 B、14，11 C、12，11 D、13，115.如图，∠1=∠2，∠3=40°，则∠4等于（ ）
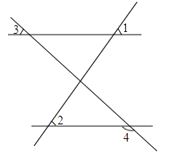A、120° B、130° C、140° D、40°6. 如图，有一矩形纸片ABCD，AB=6，AD=8，将纸片折叠使AB落在AD边上，折痕为AE，再将△ABE以BE为折痕向右折叠，AE与CD交于点F，则 的值是（ ）
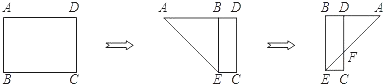A、1 B、 C、 D、7. 如图，二次函数y＝ax2＋bx＋c(a≠0)的图象的顶点在第一象限，且过点(0，1)和(－1，0)．下列结论：①ab＜0；②b2＞4a；③0＜a＋b＋c＜2；④0＜b＜1；⑤当x＞－1时，y＞0.其中正确结论的个数是（ ）
A、5个 B、4个 C、3个 D、2个二、填空题
-
8. 分解因式：ax2+2ax﹣3a= ．9. 将抛物线y=x2-2向上平移一个单位后，得一新的抛物线，那么新的抛物线的表达式是 ．10. 某商品的原价为100元，如果经过两次降价，且每次降价的百分率都是m，那么该商品现在的价格是元（结果用含m的代数式表示）．11. 若 的值为零，则x的值是 ．12. 如图，在对角线长分别为12和16的菱形ABCD中，E、F分别是边AB、AD的中点，H是对角线BD上的任意一点，则HE+HF的最小值是 ．
13. 如图，已知⊙O是以数轴的原点O为圆心，半径为1的圆，∠AOB=45°，点P在数轴上运动，若过点P且与OA平行的直线与⊙O有公共点，设OP=x，则x的取值范围是 ．
14. 如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1，5，12，22…为五边形数，则第6个五边形数是 ．
15. 在平面直角坐标系中，对于任意两点A（x1 ， y1）B （x2 ， y2），规定运算：（1）A⊕B=（x1+x2 ， y1+y2）；（2）A⊙B=x1x2+y1y2；（3）当x1=x2且y1=y2时，A=B．有下列四个命题：①若有A（1，2），B（2，﹣1），则A⊕B=（3，1），A⊙B=0；②若有A⊕B=B⊕C，则A=C；③若有A⊙B=B⊙C，则A=C；④（A⊕B）⊕C=A⊕（B⊕C）对任意点A、B、C均成立．其中正确的命题为（只填序号）
三、解答题
-
16. 计算：(1)、| ﹣2|+2 0100﹣（﹣ ）﹣1+3tan30°．(2)、 ÷（a+1）﹣ ．17. 已知：如图，点E、F分别为▱ABCD的BC、AD边上的点，且∠1=∠2．求证：AE=FC．
18. 如图，暑假快要到了，某市准备组织同学们分别到A，B，C，D四个地方进行夏令营活动，前往四个地方的人数．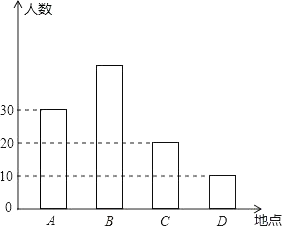
(1)、去B地参加夏令营活动人数占总人数的40%，根据统计图求去B地的人数？
(2)、若一对姐弟中只能有一人参加夏令营，姐弟俩提议让父亲决定．父亲说：现有4张卡片上分别写有1，2，3，4四个整数，先让姐姐随机地抽取一张后放回，再由弟弟随机地抽取一张．若抽取的两张卡片上的数字之和是5的倍数则姐姐参加，若抽取的两张卡片上的数字之和是3的倍数则弟弟参加．用列表法或树形图分析这种方法对姐弟俩是否公平？19. 甲、乙两名学生练习计算机打字，甲打一篇1000字的文章与乙打一篇900字的文章所用的时间相同．已知甲每分钟比乙每分钟多打5个字．问：甲、乙两人每分钟各打多少字？
20. 如图，为了测量出楼房AC的高度，从距离楼底C处60 米的点D（点D与楼底C在同一水平上）出发，沿斜面坡度为i=l： 的斜坡DB前进30米到达点B，在点B处测得楼顶A的仰角为53 ，求楼房AC的高度（参考数据：sin53 = ， cos53 = ， tan53 = ， ≈1.732，结果精确到0.1米）
21. 如图，已知反比例函数y= 的图象与直线y=﹣x+b都经过点A（1，4），且该直线与x轴的交点为B．
(1)、求反比例函数和直线的解析式；(2)、求△AOB的面积．
