四川省内江市资中县2018届九年级数学中考一模试卷

试卷更新日期：2018-08-10 类型：中考模拟

进入 出卷网 下载

一、单选题

  • 1. 下列函数中，二次函数是（   ）
    A、y=﹣4x+5 B、y=x（2x﹣3） C、y=（x+4）2﹣x2 D、y= 1x2

    查看试题解析

  • 2. 已知⊙O的半径为4cm，如果圆心O到直线l的距离为3.5cm，那么直线l与⊙O的位置关系是（   ）
    A、相交 B、相切 C、相离 D、不确定

    查看试题解析

  • 3. 抛物线y=﹣（x﹣4）2﹣5的顶点坐标和开口方向分别是（   ）
    A、（4，﹣5），开口向上 B、（4，﹣5），开口向下 C、（﹣4，﹣5），开口向上 D、（﹣4，﹣5），开口向下

    查看试题解析

  • 4. 如图，四边形ABCD内接于⊙O，E为AD延长线上一点，若∠CDE=80°，则∠B等于（   ）

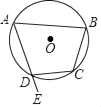    A、60° B、70° C、80° D、90°

    查看试题解析

  • 5. 在平面直角坐标系中，将抛物线y=（x+1）2向右平移2个单位，再向下平移4个单位，得到的抛物线解析式是（   ）
    A、y=（x﹣2）2﹣4 B、y=（x﹣1）2﹣4 C、y=（x﹣2）2﹣3 D、y=（x﹣1）2﹣3

    查看试题解析

  • 6. 下面四个命题中，正确的一个是（   ）
    A、平分一条弦的直径必垂直于这条弦 B、平分一条弧的直线垂直于这条弧所对的弦 C、相等圆心角所对的弧相等 D、钝角三角形的外心在三角形外

    查看试题解析

  • 7. 将二次函数y=x2﹣6x+5用配方法化成y=（x﹣h）2+ka的形式，下列结果中正确的是（   ）
    A、y=（x﹣6）2+5 B、y=（x﹣3）2+5 C、y=（x﹣3）2﹣4 D、y=（x+3）2﹣9

    查看试题解析

  • 8. 已知二次函数y=3（x﹣2）2+5，则有（   ）
    A、当x＞﹣2时，y随x的增大而减小 B、当x＞﹣2时，y随x的增大而增大 C、当x＞2时，y随x的增大而减小 D、当x＞2时，y随x的增大而增大

    查看试题解析

  • 9. 若正六边形的边长为4，则它的内切圆面积为（   ）
    A、9π B、10π C、12π D、15π

    查看试题解析

  • 10.

     如图是二次函数y=ax2+bx+c的部分图象，由图象可知不等式ax2+bx+c＜0的解集是（    ）


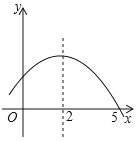    A、-1＜x＜5 B、x＞5 C、x＜-1且x＞5 D、x＜-1或x＞5

    查看试题解析

  • 11. 已知二次函数y=ax2﹣4ax+4，当x分别取x1、x2两个不同的值时，函数值相等，则当x取x1+x2时，y的值为（   ）
    A、6 B、5 C、4 D、3

    查看试题解析

  • 12. 在半径等于5cm的圆内有长为5 3 cm的弦，则此弦所对的圆周角为（   ）
    A、120° B、30°或120° C、60° D、60°或120°

    查看试题解析

二、填空题

  • 13. PA、PB分别切⊙O于点A、B，若PA=3cm，那么PB=cm．

    查看试题解析

  • 14. 抛物线y=ax2+bx+c与x轴的公共点是（﹣1，0），（3，0），则关于x的方程ax2+bx+c=0的两个根是 ．

    查看试题解析

  • 15. 已知圆锥的底面半径为5cm，侧面积为65πcm2 ， 圆锥的母线是 cm．

    查看试题解析

  • 16. 某司机驾车行驶在公路上，突然发现正前方有一行人，他迅速采取紧急刹车制动．已知，汽车刹车后行驶距离S（m）与行驶时间t（s）之间的函数关系式为S=﹣5t2+20t，则这个行人至少在米以外，司机刹车后才不会撞到行人．

    查看试题解析

  • 17. 已知△ABC内接于半径为5厘米的⊙O，若∠A=60°，边BC的长为厘米．

    查看试题解析

  • 18. 抛物线y=（2x﹣1）2+t与x轴的两个交点之间的距离为4，则t的值是 ．

    查看试题解析

  • 19. 二次函数y=ax2+bx+c（a＜0）的图象与x轴的两个交点A、B的横坐标分别为﹣3、1，与y轴交于点C，下面四个结论：①16a+4b+c＜0；②若P（﹣5，y1），Q（ 52 ，y2）是函数图象上的两点，则y1＞y2；③c=﹣3a；④若△ABC是等腰三角形，则b=﹣ 273 或﹣ 2153 ．其中正确的有 ． （请将正确结论的序号全部填在横线上）

    查看试题解析

  • 20. 如图，PA、PB切⊙O于点A、B，PA=4，∠APB=60°，点E在 AB→ 上，且CD切⊙O于点E，交PA、PB于C、D两点，则CD的最小值是 ．

    查看试题解析

三、解答题

  • 21. 已知抛物线y=﹣x2+2x+2．

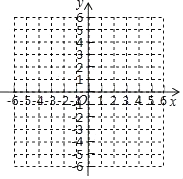    (1)、写出它的开口方向、对称轴和顶点坐标；
    (2)、在如图3的直角坐标系内画出y=﹣x2+2x+2的图象．

    查看试题解析

  • 22. 如图所示，AB是⊙O的一条弦，OD⊥AB，垂足为C，交⊙O于点D，点E在⊙O上．

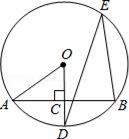    (1)、若∠AOD=52°，求∠DEB的度数；
    (2)、若OC=3，OA=5，求AB的长．

    查看试题解析

  • 23. 如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0），B（3，0）两点，与y轴交于点C（0，﹣3）．

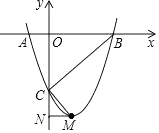    (1)、求该抛物线所对应的二次函数的表达式及顶点M的坐标；
    (2)、连结CB、CM，过点M作MN⊥y轴于点N，求证：∠BCM=90°．

    查看试题解析

  • 24. 如图，已知三角形ABC的边AB是⊙O的切线，切点为B．AC经过圆心O并与圆相交于点D、C，过C作直线CE丄AB，交AB的延长线于点E．

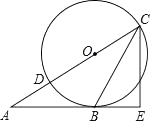    (1)、求证：CB平分∠ACE；
    (2)、若BE=3，CE=4，求⊙O的半径．

    查看试题解析

  • 25. 如图，抛物线y=﹣x2+2x的对称轴与x轴交于点A，点F在抛物线的对称轴上，且点F的纵坐标为 34 ．过抛物线上一点P（m，n）向直线y= 54 作垂线，垂足为M，连结PF．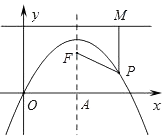

    (1)、当m=2时，求证：PF=PM；
    (2)、当点P为抛物线上任意一点时，PF=PM是否还成立？若成立，请给出证明；若不成立，请说明理由．

    查看试题解析

  • 26. 新春佳节，电子鞭炮因其安全、无污染开始走俏．某商店经销一种电子鞭炮，已知这种电子鞭炮的成本价为每盒80元，市场调查发现，该种电子鞭炮每天的销售量y（盒）与销售单价x（元）有如下关系：y=﹣2x+320（80≤x≤160）．设这种电子鞭炮每天的销售利润为w元．
    (1)、求w与x之间的函数关系式；
    (2)、该种电子鞭炮销售单价定为多少元时，每天的销售利润最大？最大利润是多少元？
    (3)、该商店销售这种电子鞭炮要想每天获得2400元的销售利润，又想买得快．那么销售单价应定为多少元？

    查看试题解析

  • 27. 如图，在⊙O中，直径AB经过弦CD的中点E，点M在OD上，AM的延长线交⊙O于点G，交过D的直线于F，且∠BDF=∠CDB，BD与CG交于点N．

    (1)、求证：DF是⊙O的切线；
    (2)、连结MN，猜想MN与AB的位置有关系，并给出证明．

    查看试题解析

  • 28. 如图，抛物线y=﹣x2+bx+c与x轴分别交于点A、B，与y轴交于点C，且OA=1，OB=3，顶点为D，对称轴交x轴于点Q．

    (1)、求抛物线对应的二次函数的表达式；
    (2)、点P是抛物线的对称轴上一点，以点P为圆心的圆经过A、B两点，且与直线CD相切，求点P的坐标；
    (3)、在抛物线的对称轴上是否存在一点M，使得△DCM∽△BQC？如果存在，求出点M的坐标；如果不存在，请说明理由．

    查看试题解析