四川成都市成华区初2018届数学第二次诊断性检测试卷
试卷更新日期：2018-08-10 类型：中考模拟
一、单选题
-
1. 中国人最先使用负数，魏晋时期的数学家刘徽在“正负术”的注文中指出，可将算筹（小棍形状的记数工具）正放表示正数，斜放表示负数．根据刘徽的这种表示法，观察图1，可推算图2中所得的数值为（ ）
A、7 B、-1 C、1 D、
2. 下面的几何体中，主视图为圆的是（ ）
A、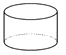
B、
C、
D、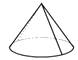
3. 下列运算正确的是（ ）
A、5ab-ab=4 B、(a2)3=a6 C、(a-b)2=a2-b2 D、4. 据相关报道，开展精准扶贫工作五年以来，我国约有55000000人摆脱贫困，将55000000用科学记数法表示是（ ）A、55×106 B、0.55×108 C、5.5×106 D、5.5×1075. 一把直尺和一块三角板ABC（其中∠B=30°，∠C=90°）摆放位置如图所示，直尺一边与三角板的两直角边分别交于点D，点E，另一边与三角板的两直角边分别交于点F，点A，且∠CDE=50°，那么∠BAF的大小为（ ）
A、20° B、40° C、45° D、50°6. 在同一平面直角坐标系中，函数y=kx(k>0）与y=(k>0)的图象可能是（ ）。
A、
B、
C、
D、
7. 某交警在一个路口统计的某时段来往车辆的车速情况如表：车速（km/h）
48
49
50
51
52
车辆数（辆）
5
4
8
2
1
则上述车速的中位数和众数分别是（ ）
A、50，8 B、49，8 C、49，50 D、50，508. 如图，在△ABC中，点D，E分别为AB，AC的中点，则△ADE与四边形BCED的面积比为（ ）
A、1：1 B、1：2 C、1：3 D、1：49. AB是⊙O的直径，PA切⊙O于点A，PO交⊙O于点C；连接BC，若∠P=40°，则∠B等于（ ）
A、20° B、25° C、30° D、40°10. 已知函数y=ax2-2ax-1（a≠0），下列四个结论：①当a =1时，函数图象经过点（-1，2）；②当 a = -2时，函数图象与x轴没有交点；③函数图象的对称轴是x = -1；④若 a＞0，则在对称轴的右侧，y随x的增大而增大．其中正确的是（ ）
A、①④ B、②③ C、①② D、③④二、填空题
-
11. 分解因式：m3﹣mn2= ．
12. 从 ，0， ， ，6这五个数中随机抽取一个数，抽到有理数的概率是 ．
13. 已知：在平行四边形ABCD中，点E在DA的延长线上，AE= AD，连接CE交BD于点F，则 的值是 ．
14. 如图，在△ABC中，∠ACB=90°，∠A=30°，BC=4，以点C为圆心，CB长为半径作弧，交AB于点D；再分别以点B和点D为圆心，大于 BD的长为半径作弧，两弧相交于点E，作射线CE交AB于点F，则AF的长为 ．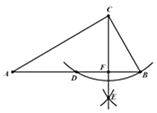
15. 若实数a，b在数轴上对应的点的位置如图，则化简 的结果是 ．
16. 若 x1 ， x2是方程x2-2mx+m2-m-1 的两个实数根，且x1+x2=1-x1x2 ，则m 的值为.
17. 有五张正面分别标有数-2，0，1，3，4的不透明卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中任取一张，将卡片上的数记为a，则使关于x的方程 有正整数解的概率为 ．
18. 如图，矩形ABCD中，AB=4，AD=8，点E，F分别在边AD，BC上，且点B，F关于过点E的直线对称，如果EF与以CD为直径的圆恰好相切，那么AE= ．
19. 如图，直线y= x-8分别交x轴，y轴于点A和点B，点C是反比例函数y= （x＞0）的图象上位于直线上方的一点，CD∥x轴交AB于D，CE⊥CD交AB于E，AD·BE=4，则k的值为 ．
三、解答题
-
20.(1)、计算：(2)、解不等式组 ，并写出该不等式组的最大整数解．21. 先化简，再求值： ，且x为满足-3＜x＜2的整数．
22. 如图，在距离铁轨200米的A处，观察由成都开往西安的“和谐号”动车，当动车车头到达B处时，车头恰好位于A处的北偏东60°方向上，10秒钟后，动车车头到达C处，此时车头恰好位于A处西偏北45°方向上，求这时段动车的平均速度是多少米/秒？（结果精确到个位，参考数据 ≈1.414， ≈1.732）
23. 九（1）班针对“你最喜爱的课外活动项目”对全班学生进行调查(每名学生分别选一个活动项目)，并根据调查结果列出统计表，绘制成扇形统计图.
根据以上信息解决下列问题：
(1)、 ， ；(2)、扇形统计图中机器人项目所对应扇形的圆心角度数为°；(3)、从选航模项目的4名学生中随机选取2名学生参加学校航模兴趣小组训练，请用列举法(画树状图或列表)求所选取的2名学生中恰好有1名男生、1名女生的概率.
24. 如图，一次函数y=ax+b与反比例函数 交于点A（1，4）和点B（-2，-2），与y轴交于点C．
(1)、求一次函数和反比例函数的解析式；(2)、点P在y轴上，且△PAB的面积等于 ，求P点的坐标．
25. 如图，AB为⊙O的直径，AC是⊙O的一条弦，D为弧BC的中点，作DE⊥AC，垂足为AC的延长线上的点E，连接DA，DB．
(1)、求证：DE为⊙O的切线；
(2)、试探究线段AB，BD，CE之间的数量关系，并说明理由；
(3)、延长ED交AB的延长线于F，若AD=DF，DE= ，求⊙O的半径 ；
26. 工人师傅用一块长为10分米，宽为8分米的矩形铁皮（厚度不计）制作一个无盖的长方体容器，如图所示，需要将四角各裁掉一个小正方形．
(1)、若长方体容器的底面面积为48平方分米，求裁掉的小正方形边长是多少分米?
(2)、若要求制作的长方体容器的底面长不大于底面宽的3倍，并将容器内部进行防锈处理，侧面每平方分米的防锈处理费用为0.5元，底面每平方分米的防锈处理费用为2元，问裁掉的正方形边长是多少分米时，总费用最低，最低费用为多少元?
27. 如图，在△ABC中，∠ACB=90°，CD是中线，AC=BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E，F，DF与AC交于点M，DE与BC交于点N．
(1)、如图1，若CE=CF，求证：DE=DF；
(2)、如图2，在∠EDF绕点D旋转的过程中：①求证：AB2=4CE•CF；
②若CE=8，CF=4，求DN的长．
28. 如图，抛物线y= x2+bx+c 与x轴交于点A和点B，与y轴交于点C，点B坐标为（6，0），点C坐标为（0，6），点D是抛物线的顶点．
(1)、求抛物线的解析式及点D的坐标；(2)、如图1，抛物线的对称轴与x轴交于点E，连接BD，点F是抛物线上的动点，当∠FBA=∠BDE时，求点F的坐标；
(3)、如图2，若点M是抛物线上的动点，过点M作MN∥x轴与抛物线交于点N，点P在x轴上，点Q在坐标平面内，以线段MN为对角线作正方形MPNQ，求点Q的坐标．