新疆乌鲁木齐市2018年中考数学试卷

试卷更新日期：2018-08-09 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣2的相反数是（）

A、﹣2 B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、2

查看试题解析
2. 如图是某个几何体的三视图，该几何体是（）

A、长方体 B、正方体 C、三棱柱 D、圆柱

查看试题解析
3. 下列运算正确的是（）

A、x³+x³=2x⁶ B、x²•x³=x⁶ C、x³÷x=x³ D、（﹣2x²）³=﹣8x⁶

查看试题解析
4. 如图把一个直角三角尺的直角顶点放在直尺的一边上，若∠1=50°，则∠2=（）

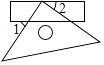A、20° B、30° C、40° D、50°

查看试题解析
5. 一个多边形的内角和是720°，这个多边形的边数是（）

A、4 B、5 C、6 D、7

查看试题解析
6. 在平面直角坐标系xOy中，将点N（﹣1，﹣2）绕点O旋转180°，得到的对应点的坐标是（）

A、（1，2） B、（﹣1，2） C、（﹣1，﹣2） D、（1，﹣2）

查看试题解析
7. 如图，在▱ABCD中，E是AB的中点，EC交BD于点F，则△BEF与△DCB的面积比为（）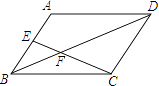

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{1}{6}$

查看试题解析
8. 甲、乙两名运动员参加射击预选赛．他们的射击成绩（单位：环）如表所示：

第一次
第二次
第三次
第四次
第五次
甲
7
9
8
6
10
乙
7
8
9
8
8
设甲、乙两人成绩的平均数分别为 $\bar{x_{甲}}$ ， $\bar{x_{乙}}$ ，方差分别s_甲² ， s_乙² ，为下列关系正确的是（）

A、 $\bar{x_{甲}}$ = $\bar{x_{乙}}$ ，s $_{甲}^{2}$ $> S_{乙}^{2}$ B、 $\bar{x_{甲}}$ = $\bar{x_{乙}}$ ，s $_{甲}^{2}$ ＜s $_{乙}^{2}$ C、 $\bar{x_{甲}}$ ＞ $\bar{x_{乙}}$ ，s $_{甲}^{2}$ ＞s $_{乙}^{2}$ D、 $\bar{x_{甲}}$ ＜ $\bar{x_{乙}}$ ，s $_{甲}^{2}$ ＜s $_{乙}^{2}$

查看试题解析
9. 宾馆有50间房供游客居住，当毎间房毎天定价为180元时，宾馆会住满；当毎间房毎天的定价每增加10元时，就会空闲一间房．如果有游客居住，宾馆需对居住的毎间房毎天支出20元的费用．当房价定为多少元时，宾馆当天的利润为10890元？设房价定为x元．则有（）

A、（180+x﹣20）（50﹣ $\frac{x}{10}$ ）=10890 B、（x﹣20）（50﹣ $\frac{x - 180}{10}$ ）=10890 C、x（50﹣ $\frac{x - 180}{10}$ ）﹣50×20=10890 D、（x+180）（50﹣ $\frac{x}{10}$ ）﹣50×20=10890

查看试题解析
10. 如图①，在矩形ABCD中，E是AD上一点，点P从点B沿折线BE﹣ED﹣DC运动到点C时停止；点Q从点B沿BC运动到点C时停止，速度均为每秒1个单位长度．如果点P、Q同时开始运动，设运动时间为t，△BPQ的面积为y，已知y与t的函数图象如图②所示．以下结论：①BC=10；②cos∠ABE= $\frac{3}{5}$ ；③当0≤t≤10时，y= $\frac{2}{5}$ t²；④当t=12时，△BPQ是等腰三角形；⑤当14≤t≤20时，y=110﹣5t中正确的有（）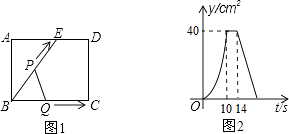

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 一个不透明的口袋中，装有5个红球，2个黄球，1个白球，这些球除颜色外完全相同，从口袋中随机摸一个球，则摸到红球的概率是．

查看试题解析
12. 不等式组 ${\begin{matrix} x + 1 > 3 (1 - x) \\ \frac{1 + 2 x}{3} \leq x \end{matrix}$ 的解集是．

查看试题解析
13. 把拋物线y=2x²﹣4x+3向左平移1个单位长度，得到的抛物线的解析式为．

查看试题解析
14. 将半径为12，圆心角为120°的扇形围成一个圆锥的侧面，则此圆锥的底面圆的半径为．

查看试题解析
15. 如图，在Rt△ABC中，∠C=90°，BC=2 $\sqrt{3}$ ，AC=2，点D是BC的中点，点E是边AB上一动点，沿DE所在直线把△BDE翻折到△B′DE的位置，B′D交AB于点F．若△AB′F为直角三角形，则AE的长为．

查看试题解析

三、解答题

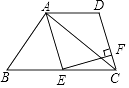
16. 计算：（ $\frac{1}{2}$ ）^﹣1﹣ $\sqrt[3]{- 8}$ +| $\sqrt{3}$ ﹣2|+2sin60°．

查看试题解析
17. 先化简，再求值：（x+1）（x﹣1）+（2x﹣1）²﹣2x（2x﹣1），其中x= $\sqrt{2}$ +1．

查看试题解析
18. 如图，在四边形ABCD中，∠BAC=90°，E是BC的中点，AD∥BC，AE∥DC，EF⊥CD于点F．

(1)、求证：四边形AECD是菱形；

(2)、若AB=6，BC=10，求EF的长．

查看试题解析
19. 某校组织学生去9km外的郊区游玩，一部分学生骑自行车先走，半小时后，其他学生乘公共汽车出发，结果他们同时到达．已知公共汽车的速度是自行车速度的3倍，求自行车的速度和公共汽车的速度分别是多少？

查看试题解析
20. 某中学1000名学生参加了”环保知识竞赛“，为了了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分取整数，满分为100分）作为样本进行统计，并制作了如图频数分布表和频数分布直方图（不完整且局部污损，其中“■”表示被污损的数据）．请解答下列问题：
成绩分组
频数
频率
50≤x＜60
8
0.16
60≤x＜70
12
a
70≤x＜80
■
0.5
80≤x＜90
3
0.06
90≤x≤100
b
c
合计
■
1

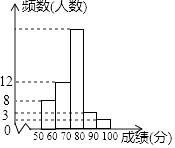(1)、写出a，b，c的值；

(2)、请估计这1000名学生中有多少人的竞赛成绩不低于70分；

(3)、在选取的样本中，从竞赛成绩是80分以上（含80分）的同学中随机抽取两名同学参加环保知识宣传活动，求所抽取的2名同学来自同一组的概率．

查看试题解析
21. 如图，小强想测量楼CD的高度，楼在围墙内，小强只能在围墙外测量，他无法测得观测点到楼底的距离，于是小强在A处仰望楼顶，测得仰角为37°，再往楼的方向前进30米至B处，测得楼顶的仰角为53°（A，B，C三点在一条直线上），求楼CD的高度（结果精确到0.1米，小强的身高忽略不计）．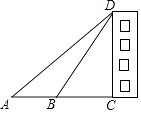

查看试题解析
22. 小明根据学习函数的经验，对y=x+ $\frac{1}{x}$ 的图象与性质进行了探究．
下面是小明的探究过程，请补充完整：

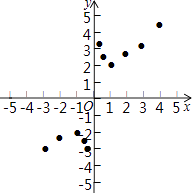(1)、函数y=x+ $\frac{1}{x}$ 的自变量x的取值范围是．

(2)、下表列出y与x的几组对应值，请写出m，n的值：m= ， n=；
x
…
﹣3
﹣2
﹣1
﹣ $\frac{1}{2}$
﹣ $\frac{1}{3}$
$\frac{1}{3}$
$\frac{1}{2}$
1
2
3
4
…
y
…
﹣ $\frac{10}{3}$
﹣ $\frac{5}{2}$
﹣2
﹣ $\frac{5}{2}$
﹣ $\frac{10}{3}$
m
$\frac{5}{2}$
2
$\frac{5}{2}$
n
$\frac{17}{4}$
…

(3)、如图．在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

(4)、结合函数的图象．请完成：
①当y=﹣ $\frac{17}{4}$ 时，x= ．
②写出该函数的一条性质．
③若方程x+ $\frac{1}{x}$ =t有两个不相等的实数根，则t的取值范围是．

查看试题解析
23. 如图，AG是∠HAF的平分线，点E在AF上，以AE为直径的⊙O交AG于点D，过点D作AH的垂线，垂足为点C，交AF于点B．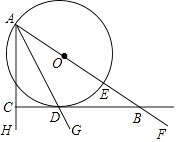

(1)、求证：直线BC是⊙O的切线；

(2)、若AC=2CD，设⊙O的半径为r，求BD的长度．

查看试题解析
24. 在平面直角坐标系xOy中，抛物线y=﹣ $\frac{1}{4}$ x²+bx+c经过点A（﹣2，0），B（8，0）．

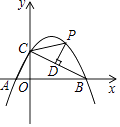(1)、求抛物线的解析式；

(2)、点C是抛物线与y轴的交点，连接BC，设点P是抛物线上在第一象限内的点，PD⊥BC，垂足为点D．
①是否存在点P，使线段PD的长度最大？若存在，请求出点P的坐标；若不存在，请说明理由；
②当△PDC与△COA相似时，求点P的坐标．

查看试题解析

	第一次	第二次	第三次	第四次	第五次
甲	7	9	8	6	10
乙	7	8	9	8	8

成绩分组	频数	频率
50≤x＜60	8	0.16
60≤x＜70	12	a
70≤x＜80	■	0.5
80≤x＜90	3	0.06
90≤x≤100	b	c
合计	■	1