四川省乐山市2018年中考数学试卷
试卷更新日期:2018-08-09 类型:中考真卷
一、选择题
-
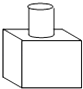
1. ﹣2的相反数是( )A、﹣2 B、2 C、 D、﹣2. 如图是由长方体和圆柱组成的几何体,它的俯视图是( )
 A、
A、 B、
B、 C、
C、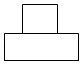 D、
D、 3. 方程组==x+y﹣4的解是( )A、 B、 C、 D、4. 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )
3. 方程组==x+y﹣4的解是( )A、 B、 C、 D、4. 如图,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是( )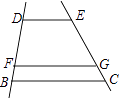 A、EG=4GC B、EG=3GC C、EG= GC D、EG=2GC5. 下列调查中,适宜采用普查方式的是( )A、调查全国中学生心理健康现状 B、调查一片试验田里五种大麦的穗长情况 C、调查冷饮市场上冰淇淋的质量情况 D、调查你所在班级的每一个同学所穿鞋子的尺码情况6. 估计 +1的值,应在( )
A、EG=4GC B、EG=3GC C、EG= GC D、EG=2GC5. 下列调查中,适宜采用普查方式的是( )A、调查全国中学生心理健康现状 B、调查一片试验田里五种大麦的穗长情况 C、调查冷饮市场上冰淇淋的质量情况 D、调查你所在班级的每一个同学所穿鞋子的尺码情况6. 估计 +1的值,应在( )
A、1和2之间 B、2和3之间 C、3和4之间 D、4和5之间7. 《九章算术》是我国古代第一部自成体系的数学专著,代表了东方数学的最高成就.它的算法体系至今仍在推动着计算机的发展和应用.书中记载:“今有圆材埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”译为:“今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯这木材,锯口深1寸(ED=1寸),锯道长1尺(AB=1尺=10寸)”,问这块圆形木材的直径是多少?”如图所示,请根据所学知识计算:圆形木材的直径AC是( )
 A、13寸 B、20寸 C、26寸 D、28寸8. 已知实数a、b满足a+b=2,ab= ,则a﹣b=( )A、1 B、﹣ C、±1 D、±9. 如图,曲线C2是双曲线C1:y= (x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于( )
A、13寸 B、20寸 C、26寸 D、28寸8. 已知实数a、b满足a+b=2,ab= ,则a﹣b=( )A、1 B、﹣ C、±1 D、±9. 如图,曲线C2是双曲线C1:y= (x>0)绕原点O逆时针旋转45°得到的图形,P是曲线C2上任意一点,点A在直线l:y=x上,且PA=PO,则△POA的面积等于( )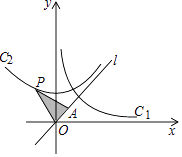 A、 B、6 C、3 D、1210. 二次函数y=x2+(a﹣2)x+3的图象与一次函数y=x(1≤x≤2)的图象有且仅有一个交点,则实数a的取值范围是( )
A、 B、6 C、3 D、1210. 二次函数y=x2+(a﹣2)x+3的图象与一次函数y=x(1≤x≤2)的图象有且仅有一个交点,则实数a的取值范围是( )
A、a=3±2 B、﹣1≤a<2 C、a=3+2 或﹣ ≤a<2 D、a=3﹣2 或﹣1≤a<﹣二、填空题
-
11. 计算:|﹣3|= .12. 化简 的结果是13. 如图,在数轴上,点A表示的数为﹣1,点B表示的数为4,C是点B关于点A的对称点,则点C表示的数为 .
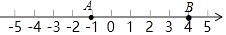 14. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠BCE的度数是度.
14. 如图,四边形ABCD是正方形,延长AB到点E,使AE=AC,连结CE,则∠BCE的度数是度. 15. 如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1, ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为 .
15. 如图,△OAC的顶点O在坐标原点,OA边在x轴上,OA=2,AC=1,把△OAC绕点A按顺时针方向旋转到△O′AC′,使得点O′的坐标是(1, ),则在旋转过程中线段OC扫过部分(阴影部分)的面积为 .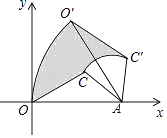 16. 已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.(1)、当k=2时,直线l1、l2与x轴围成的三角形的面积S2=;(2)、当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2 , S3 , S4 , ……,S2018 , 则S2+S3+S4+……+S2018= .
16. 已知直线l1:y=(k﹣1)x+k+1和直线l2:y=kx+k+2,其中k为不小于2的自然数.(1)、当k=2时,直线l1、l2与x轴围成的三角形的面积S2=;(2)、当k=2、3、4,……,2018时,设直线l1、l2与x轴围成的三角形的面积分别为S2 , S3 , S4 , ……,S2018 , 则S2+S3+S4+……+S2018= .三、简答题
-
17. 计算:4cos45°+(π﹣2018)0﹣18. 解不等式组:19. 如图,已知∠1=∠2,∠3=∠4,求证:BC=BD.
 20. 先化简,再求值:(2m+1)(2m﹣1)﹣(m﹣1)2+(2m)3÷(﹣8m),其中m是方程x2+x﹣2=0的根21. 某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
20. 先化简,再求值:(2m+1)(2m﹣1)﹣(m﹣1)2+(2m)3÷(﹣8m),其中m是方程x2+x﹣2=0的根21. 某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.收集数据
从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(1)、整理描述数据按如下分数段整理、描述这两组样本数据:

在表中:m= , n= .
(2)、分析数据①两组样本数据的平均数、中位数、众数如表所示:
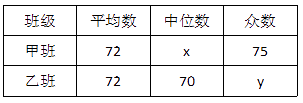
在表中:x= , y= .
②若规定测试成绩在80分(含80分)以上的叙述身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
22. 某蔬菜生产基地的气温较低时,用装有恒温系统的大棚栽培一种新品种蔬菜.如图是试验阶段的某天恒温系统从开启到关闭后,大棚内的温度y (℃)与时间x(h)之间的函数关系,其中线段AB、BC表示恒温系统开启阶段,双曲线的一部分CD表示恒温系统关闭阶段.请根据图中信息解答下列问题:
 (1)、求这天的温度y与时间x(0≤x≤24)的函数关系式;
(1)、求这天的温度y与时间x(0≤x≤24)的函数关系式;
(2)、求恒温系统设定的恒定温度;(3)、若大棚内的温度低于10℃时,蔬菜会受到伤害.问这天内,恒温系统最多可以关闭多少小时,才能使蔬菜避免受到伤害?23. 已知关于x的一元二次方程mx2+(1﹣5m)x﹣5=0(m≠0).(1)、求证:无论m为任何非零实数,此方程总有两个实数根;
(2)、若抛物线y=mx2+(1﹣5m)x﹣5与x轴交于A(x1 , 0)、B(x2 , 0)两点,且|x1﹣x2|=6,求m的值;
(3)、若m>0,点P(a,b)与Q(a+n,b)在(2)中的抛物线上(点P、Q不重合),求代数式4a2﹣n2+8n的值.24. 如图,P是⊙O外的一点,PA、PB是⊙O的两条切线,A、B是切点,PO交AB于点F,延长BO交⊙O于点C,交PA的延长交于点Q,连结AC.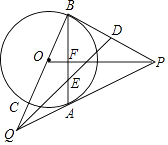 (1)、求证:AC∥PO;
(1)、求证:AC∥PO;
(2)、设D为PB的中点,QD交AB于点E,若⊙O的半径为3,CQ=2,求 的值.25. 已知Rt△ABC中,∠ACB=90°,点D、E分别在BC、AC边上,连结BE、AD交于点P,设AC=kBD,CD=kAE,k为常数,试探究∠APE的度数: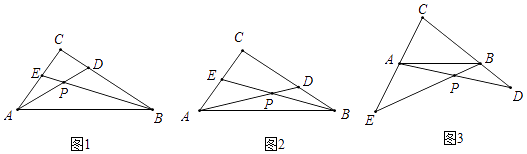 (1)、如图1,若k=1,则∠APE的度数为;(2)、如图2,若k= ,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)、如图3,若k= ,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.26. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,﹣ ),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD= .
(1)、如图1,若k=1,则∠APE的度数为;(2)、如图2,若k= ,试问(1)中的结论是否成立?若成立,请说明理由;若不成立,求出∠APE的度数.(3)、如图3,若k= ,且D、E分别在CB、CA的延长线上,(2)中的结论是否成立,请说明理由.26. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,﹣ ),OA=1,OB=4,直线l过点A,交y轴于点D,交抛物线于点E,且满足tan∠OAD= .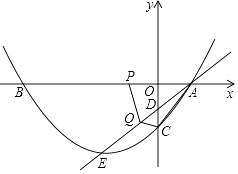 (1)、求抛物线的解析式;(2)、动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒.
(1)、求抛物线的解析式;(2)、动点P从点B出发,沿x轴正方形以每秒2个单位长度的速度向点A运动,动点Q从点A出发,沿射线AE以每秒1个单位长度的速度向点E运动,当点P运动到点A时,点Q也停止运动,设运动时间为t秒.①在P、Q的运动过程中,是否存在某一时刻t,使得△ADC与△PQA相似,若存在,求出t的值;若不存在,请说明理由.
②在P、Q的运动过程中,是否存在某一时刻t,使得△APQ与△CAQ的面积之和最大?若存在,求出t的值;若不存在,请说明理由.