山东省威海市2018年中考数学试卷

试卷更新日期：2018-08-09 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣2的绝对值是（）

A、2 B、﹣ $\frac{1}{2}$ C、 $\frac{1}{2}$ D、﹣2

查看试题解析
2. 下列运算结果正确的是（）

A、a²•a³=a⁶ B、﹣（a﹣b）=﹣a+b C、a²+a²=2a⁴ D、a⁸÷a⁴=a²

查看试题解析
3. 若点（﹣2，y₁），（﹣1，y₂），（3，y₃）在双曲线y= $\frac{k}{x}$ （k＜0）上，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₃＜y₂＜y₁ C、y₂＜y₁＜y₃ D、y₃＜y₁＜y₂

查看试题解析
4. 如图是某圆锥的主视图和左视图，该圆锥的侧面积是（）

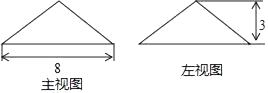A、25π B、24π C、20π D、15π

查看试题解析
5. 已知5^x=3，5^y=2，则5^2x^﹣3y=（）

A、 $\frac{3}{4}$ B、1 C、 $\frac{2}{3}$ D、 $\frac{9}{8}$

查看试题解析
6. 如图，将一个小球从斜坡的点O处抛出，小球的抛出路线可以用二次函数y=4x﹣ $\frac{1}{2}$ x²刻画，斜坡可以用一次函数y= $\frac{1}{2}$ x刻画，下列结论错误的是（）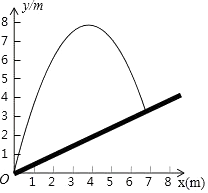

A、当小球抛出高度达到7.5m时，小球水平距O点水平距离为3m B、小球距O点水平距离超过4米呈下降趋势 C、小球落地点距O点水平距离为7米 D、斜坡的坡度为1：2

查看试题解析
7. 一个不透明的盒子中放入四张卡片，每张卡片上都写有一个数字，分别是﹣2，﹣1，0，1．卡片除数字不同外其它均相同，从中随机抽取两张卡片，抽取的两张卡片上数字之积为负数的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
8. 化简（a﹣1）÷（ $\frac{1}{a}$ ﹣1）•a的结果是（）

A、﹣a² B、1 C、a² D、﹣1

查看试题解析
9. 抛物线y=ax²+bx+c（a≠0）图象如图所示，下列结论错误的是（）

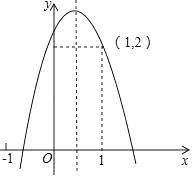A、abc＜0 B、a+c＜b C、b²+8a＞4ac D、2a+b＞0

查看试题解析
10. 如图，⊙O的半径为5，AB为弦，点C为 $\hat{A B}$ 的中点，若∠ABC=30°，则弦AB的长为（）

A、 $\frac{1}{2}$ B、5 C、 $\frac{5 \sqrt{3}}{2}$ D、5 $\sqrt{3}$

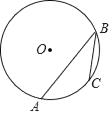查看试题解析
11. 矩形ABCD与CEFG，如图放置，点B，C，E共线，点C，D，G共线，连接AF，取AF的中点H，连接GH．若BC=EF=2，CD=CE=1，则GH=（）

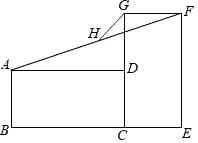A、1 B、 $\frac{2}{3}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
12. 如图，在正方形ABCD中，AB=12，点E为BC的中点，以CD为直径作半圆CFD，点F为半圆的中点，连接AF，EF，图中阴影部分的面积是（）

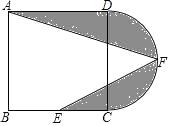A、18+36π B、24+18π C、18+18π D、12+18π

查看试题解析

二、填空题

13. 分解因式：﹣ $\frac{1}{2}$ a²+2a﹣2= ．

查看试题解析
14. 关于x的一元二次方程（m﹣5）x²+2x+2=0有实根，则m的最大整数解是．

查看试题解析
15. 如图，直线AB与双曲线y= $\frac{k}{x}$ （k＜0）交于点A，B，点P是直线AB上一动点，且点P在第二象限．连接PO并延长交双曲线于点C．过点P作PD⊥y轴，垂足为点D．过点C作CE⊥x轴，垂足为E．若点A的坐标为（﹣2，3），点B的坐标为（m，1），设△POD的面积为S₁ ， △COE的面积为S₂ ，当S₁＞S₂时，点P的横坐标x的取值范围为．

查看试题解析
16. 如图，在扇形CAB中，CD⊥AB，垂足为D，⊙E是△ACD的内切圆，连接AE，BE，则∠AEB的度数为．

查看试题解析
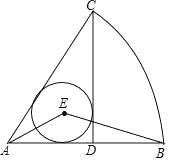17. 用若干个形状、大小完全相同的矩形纸片围成正方形，4个矩形纸片围成如图①所示的正方形，其阴影部分的面积为12；8个矩形纸片围成如图②所示的正方形，其阴影部分的面积为8；12个矩形纸片围成如图③所示的正方形，其阴影部分的面积为．

查看试题解析
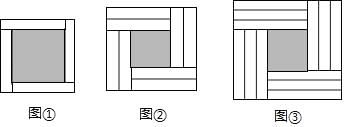18. 如图，在平面直角坐标系中，点A₁的坐标为（1，2），以点O为圆心，以OA₁长为半径画弧，交直线y= $\frac{1}{2}$ x于点B₁ ．过B₁点作B₁A₂∥y轴，交直线y=2x于点A₂ ，以O为圆心，以OA₂长为半径画弧，交直线y= $\frac{1}{2}$ x于点B₂；过点B₂作B₂A₃∥y轴，交直线y=2x于点A₃ ，以点O为圆心，以OA₃长为半径画弧，交直线y= $\frac{1}{2}$ x于点B₃；过B₃点作B₃A₄∥y轴，交直线y=2x于点A₄ ，以点O为圆心，以OA₄长为半径画弧，交直线y= $\frac{1}{2}$ x于点B₄ ， …按照如此规律进行下去，点B₂₀₁₈的坐标为．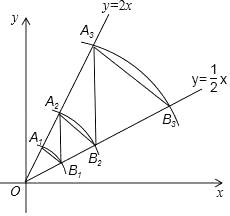

查看试题解析

三、解答题

19. 解不等式组，并将解集在数轴上表示出来．
${\begin{matrix} 2 x - 7 < 3 (x - 1) ① \\ 5 - \frac{1}{2} (x + 4) \geq x ② \end{matrix}$

查看试题解析
20. 某自动化车间计划生产480个零件，当生产任务完成一半时，停止生产进行自动化程序软件升级，用时20分钟，恢复生产后工作效率比原来提高了 $\frac{1}{3}$ ，结果完成任务时比原计划提前了40分钟，求软件升级后每小时生产多少个零件？

查看试题解析
21. 如图，将矩形ABCD（纸片）折叠，使点B与AD边上的点K重合，EG为折痕；点C与AD边上的点K重合，FH为折痕．已知∠1=67.5°，∠2=75°，EF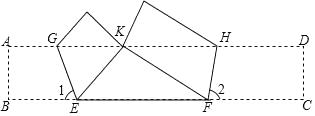= $\sqrt{3}$ +1，求BC的长．

查看试题解析
22. 为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根调查结果绘制成的统计图（部分）如图所示．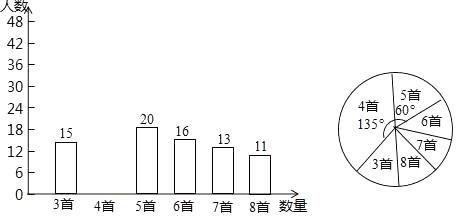
大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表
一周诗词诵背数量
3首
4首
4首
6首
7首
8首
人数
10
10
15
40
25
20
请根据调查的信息分析：

(1)、活动启动之初学生“一周诗词诵背数量”的中位数为；

(2)、估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

(3)、选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

查看试题解析
23. 为了支持大学生创业，某市政府出台了一项优惠政策：提供10万元的无息创业贷款．小王利用这笔贷款，注册了一家淘宝网店，招收5名员工，销售一种火爆的电子产品，并约定用该网店经营的利润，逐月偿还这笔无息贷款．已知该产品的成本为每件4元，员工每人每月的工资为4千元，该网店还需每月支付其它费用1万元．该产品每月销售量y（万件）与销售单价x（元）之间的函数关系如图所示．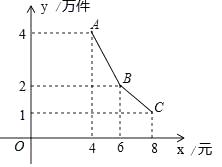

(1)、求该网店每月利润w（万元）与销售单价x（元）之间的函数表达式；

(2)、小王自网店开业起，最快在第几个月可还清10万元的无息贷款？

查看试题解析
24. 如图①，在四边形BCDE中，BC⊥CD，DE⊥CD，AB⊥AE，垂足分别为C，D，A，BC≠AC，点M，N，F分别为AB，AE，BE的中点，连接MN，MF，NF．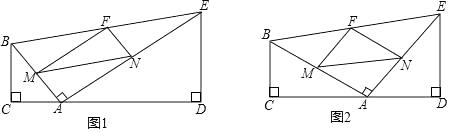

(1)、如图②，当BC=4，DE=5，tan∠FMN=1时，求 $\frac{A C}{A D}$ 的值；

(2)、若tan∠FMN= $\frac{1}{2}$ ，BC=4，则可求出图中哪些线段的长？写出解答过程；

(3)、连接CM，DN，CF，DF．试证明△FMC与△DNF全等；

(4)、在（3）的条件下，图中还有哪些其它的全等三角形？请直接写出．

查看试题解析
25. 如图，抛物线y=ax²+bx+c（a≠0）与x轴交于点A（﹣4，0），B（2，0），与y轴交于点C（0，4），线段BC的中垂线与对称轴l交于点D，与x轴交于点F，与BC交于点E，对称轴l与x轴交于点H．

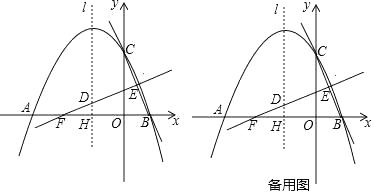(1)、求抛物线的函数表达式；

(2)、求点D的坐标；

(3)、点P为x轴上一点，⊙P与直线BC相切于点Q，与直线DE相切于点R．求点P的坐标；

(4)、点M为x轴上方抛物线上的点，在对称轴l上是否存在一点N，使得以点D，P，M．N为顶点的四边形是平行四边形？若存在，则直接写出N点坐标；若不存在，请说明理由．

查看试题解析

一周诗词诵背数量	3首	4首	4首	6首	7首	8首
人数	10	10	15	40	25	20