山东省青岛市2018年中考数学试卷
试卷更新日期:2018-08-09 类型:中考真卷
一、选择题
-
1. 观察下列四个图形,中心对称图形是( )A、
 B、
B、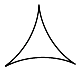 C、
C、 D、
D、 2. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )
2. 斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )
A、5×107 B、5×10﹣7 C、0.5×10﹣6 D、5×10﹣63. 如图,点A所表示的数的绝对值是( ) A、3 B、﹣3 C、 D、4. 计算(a2)3﹣5a3•a3的结果是( )
A、3 B、﹣3 C、 D、4. 计算(a2)3﹣5a3•a3的结果是( )
A、a5﹣5a6 B、a6﹣5a9 C、﹣4a6 D、4a65. 如图,点A、B、C、D在⊙O上,∠AOC=140°,点B是 的中点,则∠D的度数是( )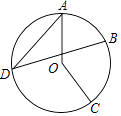 A、70° B、55° C、35.5° D、35°6. 如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF= ,则BC的长是( )
A、70° B、55° C、35.5° D、35°6. 如图,三角形纸片ABC,AB=AC,∠BAC=90°,点E为AB中点.沿过点E的直线折叠,使点B与点A重合,折痕现交于点F.已知EF= ,则BC的长是( )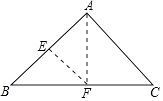 A、 B、 C、3 D、7. 如图,将线段AB绕点P按顺时针方向旋转90°,得到线段A'B',其中点A,B的对应点分别是点A',B',则点A'的坐标是( )
A、 B、 C、3 D、7. 如图,将线段AB绕点P按顺时针方向旋转90°,得到线段A'B',其中点A,B的对应点分别是点A',B',则点A'的坐标是( )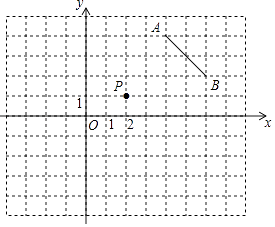 A、(﹣1,3) B、(4,0) C、(3,﹣3) D、(5,﹣1)8. 已知一次函数y= x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )
A、(﹣1,3) B、(4,0) C、(3,﹣3) D、(5,﹣1)8. 已知一次函数y= x+c的图象如图,则二次函数y=ax2+bx+c在平面直角坐标系中的图象可能是( )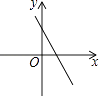 A、
A、 B、
B、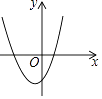 C、
C、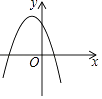 D、
D、
二、填空题
-
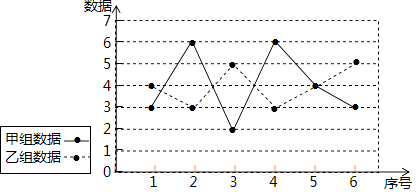
9. 已知甲、乙两组数据的折线图如图,设甲、乙两组数据的方差分别为S甲2、S乙2 , 则S甲2S乙2(填“>”、“=”、“<”)
 10. 计算:2﹣1× +2cos30°= .11. 5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少.设甲工厂5月份用水量为x吨,乙工厂5月份用水量为y吨,根据题意列关于x,y的方程组为 .
10. 计算:2﹣1× +2cos30°= .11. 5月份,甲、乙两个工厂用水量共为200吨.进入夏季用水高峰期后,两工厂积极响应国家号召,采取节水措施.6月份,甲工厂用水量比5月份减少了15%,乙工厂用水量比5月份减少了10%,两个工厂6月份用水量共为174吨,求两个工厂5月份的用水量各是多少.设甲工厂5月份用水量为x吨,乙工厂5月份用水量为y吨,根据题意列关于x,y的方程组为 .
12. 如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .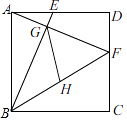 13. 如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是 .
13. 如图,Rt△ABC,∠B=90°,∠C=30°,O为AC上一点,OA=2,以O为圆心,以OA为半径的圆与CB相切于点E,与AB相交于点F,连接OE、OF,则图中阴影部分的面积是 .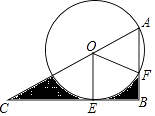 14. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.
14. 一个由16个完全相同的小立方块搭成的几何体,其最下面一层摆放了9个小立方块,它的主视图和左视图如图所示,那么这个几何体的搭法共有种.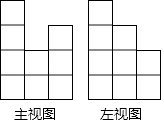
三、作图题
-
15. 已知:如图,∠ABC,射线BC上一点D.
求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.
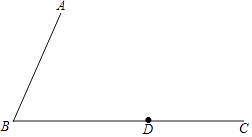
四、解答题
-
16.
(1)、解不等式组:(2)、化简:( ﹣2)• .17. 小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
18. 八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了以下统计图.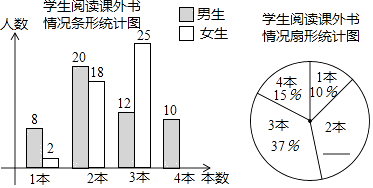
请根据图中信息解决下列问题:
(1)、共有名同学参与问卷调查;
(2)、补全条形统计图和扇形统计图;
(3)、全校共有学生1500人,请估计该校学生一个月阅读2本课外书的人数约为多少.
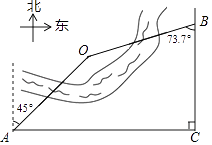
19. 某区域平面示意图如图,点O在河的一侧,AC和BC表示两条互相垂直的公路.甲勘测员在A处测得点O位于北偏东45°,乙勘测员在B处测得点O位于南偏西73.7°,测得AC=840m,BC=500m.请求出点O到BC的距离.参考数据:sin73.7°≈ ,cos73.7°≈ ,tan73.7°≈
 20. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.
20. 已知反比例函数的图象经过三个点A(﹣4,﹣3),B(2m,y1),C(6m,y2),其中m>0.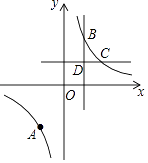 (1)、当y1﹣y2=4时,求m的值;
(1)、当y1﹣y2=4时,求m的值;
(2)、如图,过点B、C分别作x轴、y轴的垂线,两垂线相交于点D,点P在x轴上,若三角形PBD的面积是8,请写出点P坐标(不需要写解答过程).
21. 已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.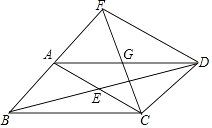 (1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
(1)、求证:AB=AF;(2)、若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.
22. 某公司投入研发费用80万元(80万元只计入第一年成本),成功研发出一种产品.公司按订单生产(产量=销售量),第一年该产品正式投产后,生产成本为6元/件.此产品年销售量y(万件)与售价x(元/件)之间满足函数关系式y=﹣x+26.
(1)、求这种产品第一年的利润W1(万元)与售价x(元/件)满足的函数关系式;
(2)、该产品第一年的利润为20万元,那么该产品第一年的售价是多少?(3)、第二年,该公司将第一年的利润20万元(20万元只计入第二年成本)再次投入研发,使产品的生产成本降为5元/件.为保持市场占有率,公司规定第二年产品售价不超过第一年的售价,另外受产能限制,销售量无法超过12万件.请计算该公司第二年的利润W2至少为多少万元.
23. 问题提出:用若干相同的一个单位长度的细直木棒,按照如图1方式搭建一个长方体框架,探究所用木棒条数的规律.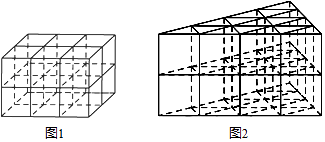
问题探究:
我们先从简单的问题开始探究,从中找出解决问题的方法.
探究一
用若干木棒来搭建横长是m,纵长是n的矩形框架(m、n是正整数),需要木棒的条数.
如图①,当m=1,n=1时,横放木棒为1×(1+1)条,纵放木棒为(1+1)×1条,共需4条;
如图②,当m=2,n=1时,横放木棒为2×(1+1)条,纵放木棒为(2+1)×1条,共需7条;
如图③,当m=2,n=2时,横放木棒为2×(2+1))条,纵放木棒为(2+1)×2条,共需12条;如图④,当m=3,n=1时,横放木棒为3×(1+1)条,纵放木棒为(3+1)×1条,共需10条;
如图⑤,当m=3,n=2时,横放木棒为3×(2+1)条,纵放木棒为(3+1)×2条,共需17条.
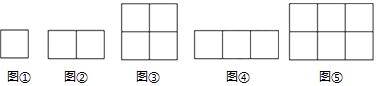
问题(一):当m=4,n=2时,共需木棒条.
问题(二):当矩形框架横长是m,纵长是n时,横放的木棒为条,
纵放的木棒为条.
探究二
用若干木棒来搭建横长是m,纵长是n,高是s的长方体框架(m、n、s是正整数),需要木棒的条数.
如图⑥,当m=3,n=2,s=1时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(1+1)=34条,竖放木棒为(3+1)×(2+1)×1=12条,共需46条;
如图⑦,当m=3,n=2,s=2时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(2+1)=51条,竖放木棒为(3+1)×(2+1)×2=24条,共需75条;
如图⑧,当m=3,n=2,s=3时,横放与纵放木棒之和为[3×(2+1)+(3+1)×2]×(3+1)=68条,竖放木棒为(3+1)×(2+1)×3=36条,共需104条.
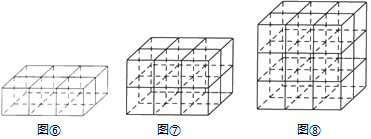
问题(三):当长方体框架的横长是m,纵长是n,高是s时,横放与纵放木棒条数之和为条,竖放木棒条数为条.
实际应用:现在按探究二的搭建方式搭建一个纵长是2、高是4的长方体框架,总共使用了170条木棒,则这个长方体框架的横长是 .
拓展应用:若按照如图2方式搭建一个底面边长是10,高是5的正三棱柱框架,需要木棒条.
24. 已知:如图,四边形ABCD,AB∥DC,CB⊥AB,AB=16cm,BC=6cm,CD=8cm,动点P从点D开始沿DA边匀速运动,动点Q从点A开始沿AB边匀速运动,它们的运动速度均为2cm/s.点P和点Q同时出发,以QA、QP为边作平行四边形AQPE,设运动的时间为t(s),0<t<5.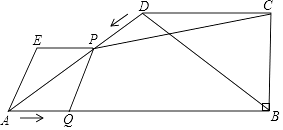
根据题意解答下列问题:
(1)、用含t的代数式表示AP;(2)、设四边形CPQB的面积为S(cm2),求S与t的函数关系式;
(3)、当QP⊥BD时,求t的值;
(4)、在运动过程中,是否存在某一时刻t,使点E在∠ABD的平分线上?若存在,求出t的值;若不存在,请说明理由.
-