山东省临沂市2018年中考数学试卷

试卷更新日期：2018-08-09 类型：中考真卷

进入出卷网下载

一、选择题

1. 在实数﹣3，﹣1，0，1中，最小的数是（）

A、﹣3 B、﹣1 C、0 D、1

查看试题解析
2. 自2013年10月习近平总书记提出“精准扶贫”的重要思想以来．各地积极推进精准扶贫，加大帮扶力度．全国脱贫人口数不断增加．仅2017年我国减少的贫困人口就接近1100万人．将1100万人用科学记数法表示为（）

A、1.1×10³人 B、1.1×10⁷人 C、1.1×10⁸人 D、11×10⁶人

查看试题解析
3. 如图，AB∥CD，∠D=42°，∠CBA=64°，则∠CBD的度数是（）

A、42° B、64° C、74° D、106°

查看试题解析
4. 一元二次方程y²﹣y﹣ $\frac{3}{4}$ =0配方后可化为（）

A、（y+ $\frac{1}{2}$ ）²=1 B、（y﹣ $\frac{1}{2}$ ）²=1 C、（y+ $\frac{1}{2}$ ）²= $\frac{3}{4}$ D、（y﹣ $\frac{1}{2}$ ）²= $\frac{3}{4}$

查看试题解析
5. 不等式组 ${\begin{matrix} 1 - 2 x < 3 \\ \frac{x + 1}{2} \leq 2 \end{matrix}$ 的正整数解的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
6. 如图．利用标杆BE测量建筑物的高度．已知标杆BE高1.2m，测得AB=1.6m．BC=12.4m．则建筑物CD的高是（）

A、9.3m B、10.5m C、12.4m D、14m

查看试题解析
7. 如图是一个几何体的三视图（图中尺寸单位：cm），根据图中所示数据求得这个几何体的侧面积是（）

A、12cm² B、（12+π）cm² C、6πcm² D、8πcm²

查看试题解析
8. 2018年某市初中学业水平实验操作考试．要求每名学生从物理、化学、生物三个学科中随机抽取一科参加测试，小华和小强都抽到物理学科的概率是（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
9. 如表是某公司员工月收入的资料．
月收入/元
45000
18000
10000
5500
5000
3400
3300
1000
人数
1
1
1
3
6
1
11
1
能够反映该公司全体员工月收入水平的统计量是（）

A、平均数和众数 B、平均数和中位数 C、中位数和众数 D、平均数和方差

查看试题解析
10. 新能源汽车环保节能，越来越受到消费者的喜爱．各种品牌相继投放市场．一汽贸公司经销某品牌新能源汽车．去年销售总额为5000万元，今年1～5月份，每辆车的销售价格比去年降低1万元．销售数量与去年一整年的相同．销售总额比去年一整年的少20%，今年1﹣5月份每辆车的销售价格是多少万元？设今年1﹣5月份每辆车的销售价格为x万元．根据题意，列方程正确的是（）

A、 $\frac{5000}{x + 1}$ = $\frac{5000 (1 - 20 %)}{x}$ B、 $\frac{5000}{x + 1}$ = $\frac{5000 (1 + 20 %)}{x}$ C、 $\frac{5000}{x - 1}$ = $\frac{5000 (1 - 20 %)}{x}$ D、 $\frac{5000}{x - 1}$ = $\frac{5000 (1 + 20 %)}{x}$

查看试题解析
11. 如图，∠ACB=90°，AC=BC．AD⊥CE，BE⊥CE，垂足分别是点D、E，AD=3，BE=1，则DE的长是（）

A、 $\frac{3}{2}$ B、2 C、2 $\sqrt{2}$ D、 $\sqrt{10}$

查看试题解析
12. 如图，正比例函y₁=k₁x与反比例函数y₂= $\frac{k_{2}}{x}$ 的图象相交于A、B两点，其中点A的横坐标为1．当y₁＜y₂时，x的取值范围是（）

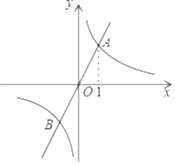A、x＜﹣1或x＞1 B、﹣1＜x＜0或x＞1 C、﹣1＜x＜0或0＜x＜1 D、x＜﹣1或0＜x＜l

查看试题解析
13. 如图，点E，F，G，H分别是四边形ABCD边AB，BC，CD，DA的中点．则下列说法：
①若AC=BD，则四边形EFGH为矩形；②若AC⊥BD，则四边形EFGH为菱形；③若四边形EFGH是平行四边形，则AC与BD互相平分；④若四边形EFGH是正方形，则AC与BD互相垂直且相等．其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
14. 一列自然数0，1，2，3，…，100．依次将该列数中的每一个数平方后除以100，得到一列新数．则下列结论正确的是（）

A、原数与对应新数的差不可能等于零 B、原数与对应新数的差，随着原数的增大而增大 C、当原数与对应新数的差等于21时，原数等于30 D、当原数取50时，原数与对应新数的差最大

查看试题解析

二、填空题

15. 计算：|1﹣ $\sqrt{2}$ |= ．

查看试题解析
16. 已知m+n=mn，则（m﹣1）（n﹣1）= ．

查看试题解析
17. 如图，在▱ABCD中，AB=10，AD=6，AC⊥BC．则BD= ．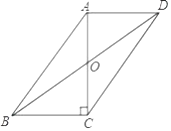

查看试题解析
18. 如图．在△ABC中，∠A=60°，BC=5cm．能够将△ABC完全覆盖的最小圆形纸片的直径是cm．

查看试题解析
19. 任何一个无限循环小数都可以写成分数的形式，应该怎样写呢？我们以无限循环小数0. $\dot{7}$ 为例进行说明：设0. $\dot{7}$ =x，由0. $\dot{7}$ =0.7777…可知，10x=7.7777…，所以10x﹣x=7，解方程，得x= $\frac{7}{9}$ ，于是．得0. $\dot{7}$ = $\frac{7}{9}$ ．将0. $\dot{3} \dot{6}$ 写成分数的形式是．

查看试题解析

三、解答题

20. 计算：（ $\frac{x + 2}{x^{2} - 2 x}$ ﹣ $\frac{x - 1}{x^{2} - 4 x + 4}$ ） $\div \frac{x - 4}{x}$ ．

查看试题解析
21. 某地某月1～20日中午12时的气温（单位：℃）如下：
22 31 25 15 18 23 21 20 27 17
20 12 18 21 21 16 20 24 26 19

(1)、将下列频数分布表补充完整：
气温分组
划记
频数
12≤x＜17
3
17≤x＜22
22≤x＜27
27≤x＜32
2

(2)、补全频数分布直方图；

(3)、根据频数分布表或频数分布直方图，分析数据的分布情况．

查看试题解析
22. 如图，有一个三角形的钢架ABC，∠A=30°，∠C=45°，AC=2（ $\sqrt{3}$ +1）m．请计算说明，工人师傅搬运此钢架能否通过一个直径为2.1m的圆形门？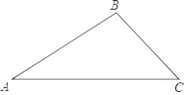

查看试题解析
23. 如图，△ABC为等腰三角形，O是底边BC的中点，腰AB与⊙O相切于点D，OB与⊙O相交于点E．

(1)、求证：AC是⊙O的切线；

(2)、若BD= $\sqrt{3}$ ，BE=1．求阴影部分的面积．

查看试题解析
24. 甲、乙两人分别从A，B两地同时出发，匀速相向而行．甲的速度大于乙的速度，甲到达B地后，乙继续前行．设出发x h后，两人相距y km，图中折线表示从两人出发至乙到达A地的过程中y与x之间的函数关系．
根据图中信息，求：

(1)、点Q的坐标，并说明它的实际意义；

(2)、甲、乙两人的速度．

查看试题解析
25. 将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．

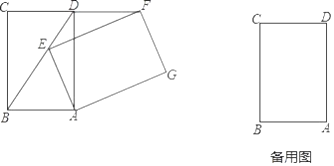(1)、如图，当点E在BD上时．求证：FD=CD；

(2)、当α为何值时，GC=GB？画出图形，并说明理由．

查看试题解析
26. 如图，在平面直角坐标系中，∠ACB=90°，OC=2OB，tan∠ABC=2，点B的坐标为（1，0）．抛物线y=﹣x²+bx+c经过A、B两点．

(1)、求抛物线的解析式；

(2)、点P是直线AB上方抛物线上的一点，过点P作PD垂直x轴于点D，交线段AB于点E，使PE= $\frac{1}{2}$ DE．
①求点P的坐标；
②在直线PD上是否存在点M，使△ABM为直角三角形？若存在，求出符合条件的所有点M的坐标；若不存在，请说明理由．

查看试题解析

月收入/元	45000	18000	10000	5500	5000	3400	3300	1000
人数	1	1	1	3	6	1	11	1

气温分组	划记	频数
12≤x＜17		3
17≤x＜22
22≤x＜27
27≤x＜32		2