内蒙古包头市2018年中考数学试卷
试卷更新日期:2018-08-09 类型:中考真卷
一、选择题
-
1. 计算﹣ ﹣|﹣3|的结果是( )
A、﹣1 B、﹣5 C、1 D、52. 如图,是由几个大小相同的小立方块所搭几何体的俯视图,其中小正方形中的数字表示在该位置的小立方块的个数,则这个几何体的主视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 函数y= 中,自变量x的取值范围是( )
3. 函数y= 中,自变量x的取值范围是( )
A、x≠1 B、x>0 C、x≥1 D、x>14. 下列事件中,属于不可能事件的是( )
A、某个数的绝对值大于0 B、某个数的相反数等于它本身 C、任意一个五边形的外角和等于540° D、长分别为3,4,6的三条线段能围成一个三角形5. 如果2xa+1y与x2yb﹣1是同类项,那么 的值是( )
A、 B、 C、1 D、36. 一组数据1,3,4,4,4,5,5,6的众数和方差分别是( )
A、4,1 B、4,2 C、5,1 D、5,27. 如图,在△ABC中,AB=2,BC=4,∠ABC=30°,以点B为圆心,AB长为半径画弧,交BC于点D,则图中阴影部分的面积是( )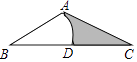 A、2﹣ B、2﹣ C、4﹣ D、4﹣8. 如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )
A、2﹣ B、2﹣ C、4﹣ D、4﹣8. 如图,在△ABC中,AB=AC,△ADE的顶点D,E分别在BC,AC上,且∠DAE=90°,AD=AE.若∠C+∠BAC=145°,则∠EDC的度数为( )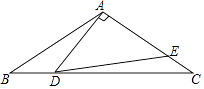 A、17.5° B、12.5° C、12° D、10°9. 已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A、17.5° B、12.5° C、12° D、10°9. 已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A、6 B、5 C、4 D、310. 已知下列命题:①若a3>b3 , 则a2>b2;②若点A(x1 , y1)和点B(x2 , y2)在二次函数y=x2﹣2x﹣1的图象上,且满足x1<x2<1,则y1>y2>﹣2;③在同一平面内,a,b,c是直线,且a∥b,b⊥c,则a∥c;④周长相等的所有等腰直角三角形全等.其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个11. 如图,在平面直角坐标系中,直线l1:y=﹣ x+1与x轴,y轴分别交于点A和点B,直线l2:y=kx(k≠0)与直线l1在第一象限交于点C.若∠BOC=∠BCO,则k的值为( )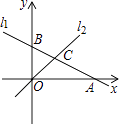 A、 B、 C、 D、212. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )
A、 B、 C、 D、212. 如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为( )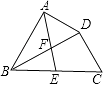 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若a﹣3b=2,3a﹣b=6,则b﹣a的值为 .
14. 不等式组 的非负整数解有个.
15. 从﹣2,﹣1,1,2四个数中,随机抽取两个数相乘,积为大于﹣4小于2的概率是 .
16. 化简; ÷( ﹣1)= .
17. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线与BA的延长线交于点D,点E在 上(不与点B,C重合),连接BE,CE.若∠D=40°,则∠BEC=度.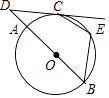 18. 如图,在▱ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为 .
18. 如图,在▱ABCD中,AC是一条对角线,EF∥BC,且EF与AB相交于点E,与AC相交于点F,3AE=2EB,连接DF.若S△AEF=1,则S△ADF的值为 .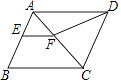 19. 以矩形ABCD两条对角线的交点O为坐标原点,以平行于两边的方向为坐标轴,建立如图所示的平面直角坐标系,BE⊥AC,垂足为E.若双曲线y= (x>0)经过点D,则OB•BE的值为 .
19. 以矩形ABCD两条对角线的交点O为坐标原点,以平行于两边的方向为坐标轴,建立如图所示的平面直角坐标系,BE⊥AC,垂足为E.若双曲线y= (x>0)经过点D,则OB•BE的值为 . 20. 如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:
20. 如图,在Rt△ACB中,∠ACB=90°,AC=BC,D是AB上的一个动点(不与点A,B重合),连接CD,将CD绕点C顺时针旋转90°得到CE,连接DE,DE与AC相交于点F,连接AE.下列结论:①△ACE≌△BCD;②若∠BCD=25°,则∠AED=65°;③DE2=2CF•CA;④若AB=3 ,AD=2BD,则AF= .其中正确的结论是 . (填写所有正确结论的序号)

三、解答题
-
21. 某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
修造人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)、直接写出这四名候选人面试成绩的中位数;
(2)、现得知候选人丙的综合成绩为87.6分,求表中x的值;(3)、求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
22. 如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=AD,连接BD,点E在AB上,且∠BDE=15°,DE=4 ,DC=2 .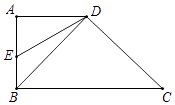
(注意:本题中的计算过程和结果均保留根号)
(1)、求BE的长;(2)、求四边形DEBC的面积.23. 某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)、求该商店3月份这种商品的售价是多少元?(2)、如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?
24. 如图,在Rt△ACB中,∠ACB=90°,以点A为圆心,AC长为半径的圆交AB于点D,BA的延长线交⊙A于点E,连接CE,CD,F是⊙A上一点,点F与点C位于BE两侧,且∠FAB=∠ABC,连接BF.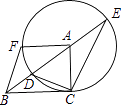 (1)、求证:∠BCD=∠BEC;(2)、若BC=2,BD=1,求CE的长及sin∠ABF的值.25. 如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.
(1)、求证:∠BCD=∠BEC;(2)、若BC=2,BD=1,求CE的长及sin∠ABF的值.25. 如图,在矩形ABCD中,AB=3,BC=5,E是AD上的一个动点.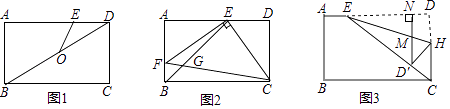 (1)、如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;(2)、如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;(3)、如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.
(1)、如图1,连接BD,O是对角线BD的中点,连接OE.当OE=DE时,求AE的长;(2)、如图2,连接BE,EC,过点E作EF⊥EC交AB于点F,连接CF,与BE交于点G.当BE平分∠ABC时,求BG的长;(3)、如图3,连接EC,点H在CD上,将矩形ABCD沿直线EH折叠,折叠后点D落在EC上的点D'处,过点D′作D′N⊥AD于点N,与EH交于点M,且AE=1.①求 的值;
②连接BE,△D'MH与△CBE是否相似?请说明理由.
26. 如图,在平面直角坐标系中,已知抛物线y= x2+ x﹣2与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,直线l经过A,C两点,连接BC.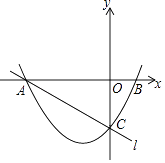 (1)、求直线l的解析式;(2)、若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)、取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、求直线l的解析式;(2)、若直线x=m(m<0)与该抛物线在第三象限内交于点E,与直线l交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)、取点G(0,﹣1),连接AG,在第一象限内的抛物线上,是否存在点P,使∠BAP=∠BCO﹣∠BAG?若存在,求出点P的坐标;若不存在,请说明理由.