辽宁省大连市2018年中考数学试卷
试卷更新日期：2018-08-09 类型：中考真卷
一、选择题
-
1. ﹣3的绝对值是（ ）A、3 B、﹣3 C、 D、-2. 在平面直角坐标系中，点（﹣3，2）所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 计算（x3）2的结果是（ ）A、x5 B、2x3 C、x9 D、x64. 如图是用直尺和一个等腰直角三角尺画平行线的示意图，图中∠α的度数为（ ）
A、45° B、60° C、90° D、135°5. 一个几何体的三视图如图所示，则这个几何体是（ ）
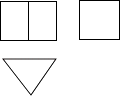A、圆柱 B、圆锥 C、三棱柱 D、长方体6. 如图，菱形ABCD中，对角线AC，BD相交于点O，若AB=5，AC=6，则BD的长是（ ）
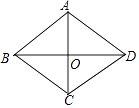A、8 B、7 C、4 D、37. 一个不透明的袋子中有三个完全相同的小球，把它们分别标号为1，2，3，随机摸出一个小球，记下标号后放回，再随机摸出一个小球并记下标号，两次摸出的小球标号的和是偶数的概率是（ ）A、 B、 C、 D、8. 如图，有一张矩形纸片，长10cm，宽6cm，在它的四角各减去一个同样的小正方形，然后折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是32cm2 ， 求剪去的小正方形的边长．设剪去的小正方形边长是xcm，根据题意可列方程为（ ）
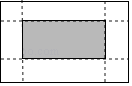A、10×6﹣4×6x=32 B、（10﹣2x）（6﹣2x）=32 C、（10﹣x）（6﹣x）=32 D、10×6﹣4x2=329. 如图，一次函数y=k1x+b的图象与反比例函数y= 的图象相交于A（2，3），B（6，1）两点，当k1x+b＜ 时，x的取值范围为（ ）
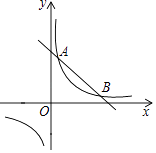A、x＜2 B、2＜x＜6 C、x＞6 D、0＜x＜2或x＞610. 如图，将△ABC绕点B逆时针旋转α，得到△EBD，若点A恰好在ED的延长线上，则∠CAD的度数为（ ）
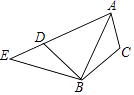A、90°﹣α B、α C、180°﹣α D、2α二、填空题
-
11. 因式分解：x2﹣x= ．12. 五名学生一分钟跳绳的次数分别为189，195，163，184，201，该组数据的中位数是 ．13. 一个扇形的圆心角为120°，它所对的弧长为6πcm，则此扇形的半径为cm．14. 《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？设有x匹大马，y匹小马，根据题意可列方程组为 ．
15. 如图，小明为了测量校园里旗杆AB的高度，将测角仪CD竖直放在距旗杆底部B点6m的位置，在D处测得旗杆顶端A的仰角为53°，若测角仪的高度是1.5m，则旗杆AB的高度约为m．（精确到0.1m．参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）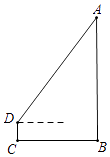
16. 如图，矩形ABCD中，AB=2，BC=3，点E为AD上一点，且∠ABE=30°，将△ABE沿BE翻折，得到△A′BE，连接CA′并延长，与AD相交于点F，则DF的长为 ．
三、解答题
-
17. 计算：（ +2）2﹣ +2﹣218. 解不等式组：19. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AF=CE．
求证：BE=DF．
20. 某校为了解学生最喜欢的球类运动情况，随机选取该校部分学生进行调查，要求每名学生只写一类最喜欢的球类运动．以下是根据调查结果绘制的统计图表的一部分．
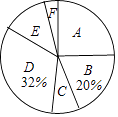
根据以上信息，解答下列问题：
(1)、被调查的学生中，最喜欢乒乓球的有人，最喜欢篮球的学生数占被调查总人数的百分比为%；(2)、被调查学生的总数为人，其中，最喜欢篮球的有人，最喜欢足球的学生数占被调查总人数的百分比为%；(3)、该校共有450名学生，根据调查结果，估计该校最喜欢排球的学生数．
四、解答题
-
21. 甲、乙两名学生练习打字，甲打135个字所用时间与乙打180个字所用时间相同．已知甲平均每分钟比乙少打20个字，求甲平均每分钟打字的个数．
22. 【观察】1×49=49，2×48=96，3×47=141，…，23×27=621，24×26=624，25×25=625，26×24=624，27×23=621，…，47×3=141，28×2=96，49×1=49．(1)、【发现】根据你的阅读回答问题：①上述内容中，两数相乘，积的最大值为；
②设参与上述运算的第一个因数为a，第二个因数为b，用等式表示a与b的数量关系是 ．
(2)、【类比】观察下列两数的积：1×59，2×58，3×57，4×56，…，m×n，…，56×4，57×3，58×2，59×1．猜想mn的最大值为 ， 并用你学过的知识加以证明．
23. 如图，四边形ABCD内接于⊙O，∠BAD=90°，点E在BC的延长线上，且∠DEC=∠BAC．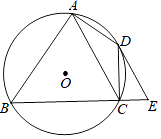
(1)、求证：DE是⊙O的切线；(2)、若AC∥DE，当AB=8，CE=2时，求AC的长．五、解答题
-
24. 如图1，直线AB与x轴、y轴分别相交于点A、B，将线段AB绕点A顺时针旋转90°，得到AC，连接BC，将△ABC沿射线BA平移，当点C到达x轴时运动停止．设平移距离为m，平移后的图形在x轴下方部分的面积为S，S关于m的函数图象如图2所示（其中0＜m≤a，a＜m≤b时，函数的解析式不同）．
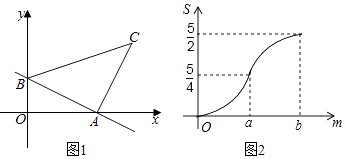(1)、填空：△ABC的面积为；(2)、求直线AB的解析式；(3)、求S关于m的解析式，并写出m的取值范围．25. 阅读下面材料：小明遇到这样一个问题：
如图1，△ABC中，∠ACB=90°，点D在AB上，且∠BAC=2∠DCB，求证：AC=AD．
小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：
方法1：如图2，作AE平分∠CAB，与CD相交于点E．
方法2：如图3，作∠DCF=∠DCB，与AB相交于点F．
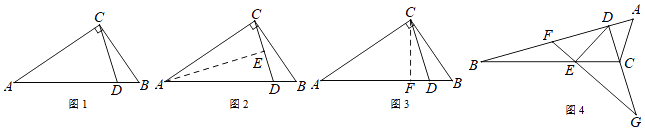(1)、根据阅读材料，任选一种方法，证明AC=AD．用学过的知识或参考小明的方法，解决下面的问题：
(2)、如图4，△ABC中，点D在AB上，点E在BC上，且∠BDE=2∠ABC，点F在BD上，且∠AFE=∠BAC，延长DC、FE，相交于点G，且∠DGF=∠BDE．①在图中找出与∠DEF相等的角，并加以证明；②若AB=kDF，猜想线段DE与DB的数量关系，并证明你的猜想．26. 如图，点A，B，C都在抛物线y=ax2﹣2amx+am2+2m﹣5（其中﹣ ＜a＜0）上，AB∥x轴，∠ABC=135°，且AB=4．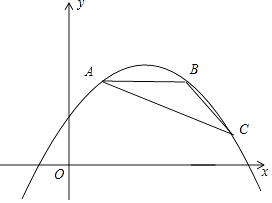
(1)、填空：抛物线的顶点坐标为（用含m的代数式表示）；(2)、求△ABC的面积（用含a的代数式表示）；(3)、若△ABC的面积为2，当2m﹣5≤x≤2m﹣2时，y的最大值为2，求m的值．