江苏省常州市2018年中考数学试卷

试卷更新日期：2018-08-09 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣3的倒数是（）

A、﹣3 B、3 C、﹣ $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 已知苹果每千克m元，则2千克苹果共多少元？（）

A、m﹣2 B、m+2 C、 $\frac{m}{2}$ D、2m

查看试题解析
3. 下列图形中，哪一个是圆锥的侧面展开图？（）

A、 B、 C、 D、

查看试题解析
4. 一个正比例函数的图象经过（2，﹣1），则它的表达式为（）

A、y=﹣2x B、y=2x C、 $y = - \frac{1}{2} x$ D、 $y = \frac{1}{2} x$

查看试题解析
5. 下列命题中，假命题是（）

A、一组对边相等的四边形是平行四边形 B、三个角是直角的四边形是矩形 C、四边相等的四边形是菱形 D、有一个角是直角的菱形是正方形

查看试题解析
6. 已知a为整数，且 $\sqrt{3} < a < \sqrt{5}$ ，则a等于（）

A、1 B、2 C、3 D、4

查看试题解析
7. 如图，AB是⊙O的直径，MN是⊙O的切线，切点为N，如果∠MNB=52°，则∠NOA的度数为（）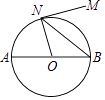

A、76° B、56° C、54° D、52°

查看试题解析
8. 某数学研究性学习小组制作了如下的三角函数计算图尺：在半径为1的半圆形量角器中，画一个直径为10的圆，把刻度尺CA的0刻度固定在半圆的圆心O处，刻度尺可以绕点O旋转．从图中所示的图尺可读出sin∠AOB的值是（）

A、 $\frac{5}{8}$ B、 $\frac{7}{8}$ C、 $\frac{7}{10}$ D、 $\frac{4}{5}$

查看试题解析

二、填空题

9. 计算：|﹣3|﹣1= ．

查看试题解析
10. 化简： $\frac{a}{a - b} - \frac{b}{a - b}$ = ．

查看试题解析
11. 分解因式：3x²﹣6x+3= ．

查看试题解析
12. 已知点P（﹣2，1），则点P关于x轴对称的点的坐标是．

查看试题解析
13. 地球与月球的平均距离大约384000km，用科学记数法表示这个距离为km．

查看试题解析
14. 中华文化源远流长，如图是中国古代文化符号的太极图，圆中的黑色部分和白色部分关于圆心中心对称．在圆内随机取一点，则此点取黑色部分的概率是．

查看试题解析
15. 如图，在▱ABCD中，∠A=70°，DC=DB，则∠CDB= ．

查看试题解析
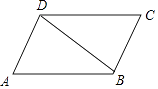16. 如图，△ABC是⊙O的内接三角形，∠BAC=60°， $\hat{B C}$ 的长是 $\frac{4 π}{3}$ ，则⊙O的半径是．

查看试题解析
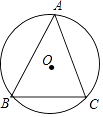17. 下面是按一定规律排列的代数式：a² ， 3a⁴ ， 5a⁶ ， 7a⁸ ， …则第8个代数式是．

查看试题解析
18. 如图，在△ABC纸板中，AC=4，BC=2，AB=5，P是AC上一点，过点P沿直线剪下一个与△ABC相似的小三角形纸板，如果有4种不同的剪法，那么AP长的取值范围是．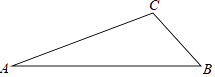

查看试题解析

三、解答题

19. 计算：|﹣1|﹣ $\sqrt{4}$ ﹣（1﹣ $\sqrt{2}$ ）⁰+4sin30°．

查看试题解析
20. 解方程组和不等式组：

(1)、 ${\begin{matrix} 2 x - 3 y = 7 \\ x + 3 y = - 1 \end{matrix}$

(2)、 ${\begin{matrix} 2 x - 6 \geq 0 \\ x + 2 \geq - x \end{matrix}$

查看试题解析
21. 如图，把△ABC沿BC翻折得△DBC．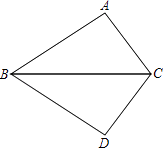

(1)、连接AD，则BC与AD的位置关系是．

(2)、不在原图中添加字母和线段，只加一个条件使四边形ABDC是平行四边形，写出添加的条件，并说明理由．

查看试题解析
22. 为了解某市初中学生课外阅读情况，调查小组对该市这学期初中学生阅读课外书籍的册数进行了抽样调查，并根据调查结果绘制成如下统计图．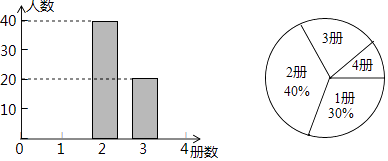
根据统计图提供的信息，解答下列问题：

(1)、本次抽样调查的样本容量是；

(2)、补全条形统计图；

(3)、该市共有12000名初中生，估计该市初中学生这学期课外阅读超过2册的人数．

查看试题解析
23. 将图中的A型、B型、C型矩形纸片分别放在3个盒子中，盒子的形状、大小、质地都相同，再将这3个盒子装入一只不透明的袋子中．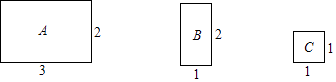

(1)、搅匀后从中摸出1个盒子，求摸出的盒子中是A型矩形纸片的概率；

(2)、搅匀后先从中摸出1个盒子（不放回），再从余下的两个盒子中摸出一个盒子，求2次摸出的盒子的纸片能拼成一个新矩形的概率（不重叠无缝隙拼接）．

查看试题解析
24. 如图，已知点A在反比例函数y= $\frac{4}{x}$ （x＞0）的图象上，过点A作AC⊥x轴，垂足是C，AC=OC．一次函数y=kx+b的图象经过点A，与y轴的正半轴交于点B．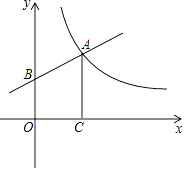

(1)、求点A的坐标；

(2)、若四边形ABOC的面积是3，求一次函数y=kx+b的表达式．

查看试题解析
25. 京杭大运河是世界文化遗产．综合实践活动小组为了测出某段运河的河宽（岸沿是平行的），如图，在岸边分别选定了点A、B和点C、D，先用卷尺量得AB=160m，CD=40m，再用测角仪测得∠CAB=30°，∠DBA=60°，求该段运河的河宽（即CH的长）．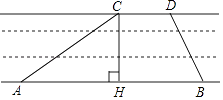

查看试题解析
26. 阅读材料：各类方程的解法
求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想转化，把未知转化为已知．
用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x³+x²﹣2x=0，可以通过因式分解把它转化为x（x²+x﹣2）=0，解方程x=0和x²+x﹣2=0，可得方程x³+x²﹣2x=0的解．

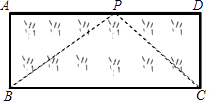(1)、问题：方程x³+x²﹣2x=0的解是x₁=0，x₂= ， x₃=；

(2)、拓展：用“转化”思想求方程 $\sqrt{2 x + 3}$ =x的解；

(3)、应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长．

查看试题解析
27. 如图

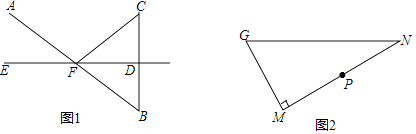(1)、如图1，已知EK垂直平分BC，垂足为D，AB与EK相交于点F，连接CF．求证：∠AFE=∠CFD．

(2)、如图2，在Rt△GMN中，∠M=90°，P为MN的中点．
①用直尺和圆规在GN边上求作点Q，使得∠GQM=∠PQN（保留作图痕迹，不要求写作法）；
②在①的条件下，如果∠G=60°，那么Q是GN的中点吗？为什么？

查看试题解析
28. 如图，二次函数y=﹣ $\frac{1}{3} x^{2}$ +bx+2的图象与x轴交于点A、B，与y轴交于点C，点A的坐标为（﹣4，0），P是抛物线上一点（点P与点A、B、C不重合）．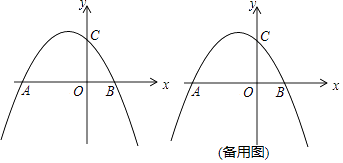

(1)、b= ，点B的坐标是；

(2)、设直线PB与直线AC相交于点M，是否存在这样的点P，使得PM：MB=1：2？若存在求出点P的横坐标；若不存在，请说明理由；

(3)、连接AC、BC，判断∠CAB和∠CBA的数量关系，并说明理由．

查看试题解析