湖南省张家界市2018年中考数学试卷

试卷更新日期：2018-08-09 类型：中考真卷

进入出卷网下载

一、选择题

1. 2018的绝对值是（）

A、 2018 B、﹣2018 C、 $\frac{1}{2018}$ D、 $- \frac{1}{2018}$

查看试题解析
2. 若关于x的分式方程 $\frac{m - 3}{x - 1}$ =1的解为x=2，则m的值为（）

A、5 B、4 C、3 D、2

查看试题解析
3. 下列图形中，既是中心对称图形，又是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、a²+a=2a³ B、 $\sqrt{a^{2}}$ =a C、（a+1）²=a²+1 D、（a³）²=a⁶

查看试题解析
5. 若一组数据a₁ ， a₂ ， a₃的平均数为4，方差为3，那么数据a₁+2，a₂+2，a₃+2的平均数和方差分别是（）

A、4，3 B、6，3 C、3，4 D、6，5

查看试题解析
6. 如图，AB是⊙O的直径，弦CD⊥AB于点E，OC=5cm，CD=8cm，则AE=（）

A、8cm B、5cm C、3cm D、2cm

查看试题解析
7. 下列说法中，正确的是（）

A、两条直线被第三条直线所截，内错角相等 B、对角线相等的平行四边形是正方形 C、相等的角是对顶角 D、角平分线上的点到角两边的距离相等

查看试题解析
8. 观察下列算式：2¹=2，2²=4，2³=8，2⁴=16，2⁵=32，2⁶=64，2⁷=128，2⁸=256…，则2+2²+2³+2⁴+2⁵+…+2¹⁰¹⁸的末位数字是（）

A、8 B、6 C、4 D、0

查看试题解析

二、填空题

9. 因式分解：a²+2a+1= ．

查看试题解析
10. 目前世界上能制造的芯片最小工艺水平是5纳米，而我国能制造芯片的最小工艺水平是16纳米，已知1纳米=10^﹣9米，用科学记数法将16纳米表示为米．

查看试题解析
11. 在一个不透明的袋子里装有3个白色乒乓球和若干个黄色乒乓球，若从这个袋子里随机摸岀一个乒乓球，恰好是黄球的概率为 $\frac{7}{10}$ ，则袋子内共有乒乓球的个数为．

查看试题解析
12. 如图，将△ABC绕点A逆时针旋转150°，得到△ADE，这时点B，C，D恰好在同一直线上，则∠B的度数为．

查看试题解析
13. 关于x的一元二次方程x²﹣kx+1=0有两个相等的实数根，则k= ．

查看试题解析
14. 如图，矩形ABCD的边AB与x轴平行，顶点A的坐标为（2，1），点B与点D都在反比例函数y= $\frac{6}{x}$ （x＞0）的图象上，则矩形ABCD的周长为．

查看试题解析

三、解答题

15. （ $\sqrt{3}$ ﹣1）⁰+（﹣1）^﹣2﹣4sin60°+ $\sqrt{12}$ ．

查看试题解析
16. 解不等式组 ${\begin{matrix} 2 x - 1 < 5 \\ x + 2 \geq 1 \end{matrix}$ ，写出其整数解．

查看试题解析
17. 在矩形ABCD中，点E在BC上，AE=AD，DF⊥AE，垂足为F．

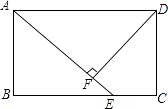(1)、求证．DF=AB；

(2)、若∠FDC=30°，且AB=4，求AD．

查看试题解析
18. 列方程解应用题
《九章算术》中有“盈不足术”的问题，原文如下：“今有共買羊，人出五，不足四十五；人出七，不足三．问人数、羊價各幾何？”题意是：若干人共同出资买羊，每人出5元，则差45元；每人出7元，则差3元．求人数和羊价各是多少？

查看试题解析
19. 阅读理解题
在平面直角坐标系xOy中，点P（x₀ ， y₀）到直线Ax+By+C=0（A²+B²≠0）的距离公式为：d= $\frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$ ，
例如，求点P（1，3）到直线4x+3y﹣3=0的距离．
解：由直线4x+3y﹣3=0知：A=4，B=3，C=﹣3
所以P（1，3）到直线4x+3y﹣3=0的距离为：d= $\frac{| 4 \times 1 + 3 \times 3 - 3 |}{\sqrt{4^{2} + 3^{2}}}$ =2
根据以上材料，解决下列问题：

(1)、求点P₁（0，0）到直线3x﹣4y﹣5=0的距离．

(2)、若点P₂（1，0）到直线x+y+C=0的距离为 $\sqrt{2}$ ，求实数C的值．

查看试题解析
20. 如图，点P是⊙O的直径AB延长线上一点，且AB=4，点M为 $\hat{A B}$ 上一个动点（不与A，B重合），射线PM与⊙O交于点N（不与M重合）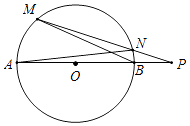

(1)、当M在什么位置时，△MAB的面积最大，并求岀这个最大值；

(2)、求证：△PAN∽△PMB．

查看试题解析
21. 今年是我市全面推进中小学校“社会主义核心价值观”教育年．某校对全校学生进行了中期检测评价，检测结果分为A（优秀）、B（良好）、C（合格）、D（不合格）四个等级．并随机抽取若干名学生的检测结果作为样本进行数据处理，制作了如下所示不完整的统计表（图1）和统计图（图2）．
等级
频数
频率
A
a
0.3
B
35
0.35
C
31
b
D
4
0.04
请根据图提供的信息，解答下列问题：

(1)、本次随机抽取的样本容量为；

(2)、a= ， b=；

(3)、请在图2中补全条形统计图；

(4)、若该校共有学生800人，据此估算，该校学生在本次检测中达到“A（优秀）”等级的学生人数为人．

查看试题解析
22. 2017年9月8日﹣10日，第六届翼装飞行世界锦标赛在我市天门山风景区隆重举行，来自全球11个国家的16名选手参加了激烈的角逐．如图，某选手从离水平地面1000米高的A点出发（AB=1000米），沿俯角为30°的方向直线飞行1400米到达D点，然后打开降落伞沿俯角为60°的方向降落到地面上的C点，求该选手飞行的水平距离BC．

查看试题解析
23. 如图，已知二次函数y=ax²+1（a≠0，a为实数）的图象过点A（﹣2，2），一次函数y=kx+b（k≠0，k，b为实数）的图象l经过点B（0，2）．

(1)、求a值并写出二次函数表达式；

(2)、求b值；

(3)、设直线l与二次函数图象交于M，N两点，过M作MC垂直x轴于点C，试证明：MB=MC；

(4)、在（3）的条件下，请判断以线段MN为直径的圆与x轴的位置关系，并说明理由．

查看试题解析

等级	频数	频率
A	a	0.3
B	35	0.35
C	31	b
D	4	0.04