贵州省安顺市2018年中考数学试卷
试卷更新日期:2018-08-09 类型:中考真卷
一、选择题
-
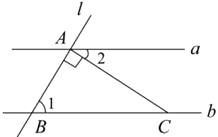
1. 的算术平方根为( )A、 B、 C、 D、22. “五·一”期间,美丽的黄果树瀑布景区吸引大量游客前来游览.经统计,某段时间内来该风景区游览的人数约为36000人,用科学记数法表示36000为( )A、 B、 C、 D、3. 如图,直线 ,直线l与直线a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若 ,则 的度数为( )
 A、 B、 C、 D、4. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下哪个条件仍不能判定 ( )
A、 B、 C、 D、4. 如图,点D,E分别在线段AB,AC上,CD与BE相交于O点,已知AB=AC,现添加以下哪个条件仍不能判定 ( )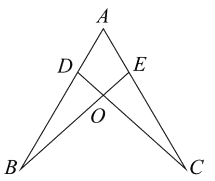 A、 B、AD=AE C、BD=CE D、BE=CD5. 一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是( )A、12 B、9 C、13 D、12或96. 要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )A、在某中学抽取200名女生 B、在安顺市中学生中抽取200名学生 C、在某中学抽取200名学生 D、在安顺市中学生中抽取200名男生7. 已知 ,用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、
A、 B、AD=AE C、BD=CE D、BE=CD5. 一个等腰三角形的两条边长分别是方程 的两根,则该等腰三角形的周长是( )A、12 B、9 C、13 D、12或96. 要调查安顺市中学生了解禁毒知识的情况,下列抽样调查最适合的是( )A、在某中学抽取200名女生 B、在安顺市中学生中抽取200名学生 C、在某中学抽取200名学生 D、在安顺市中学生中抽取200名男生7. 已知 ,用尺规作图的方法在BC上确定一点P,使PA+PC=BC,则符合要求的作图痕迹是( )A、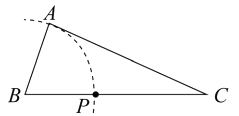 B、
B、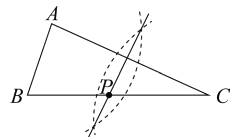 C、
C、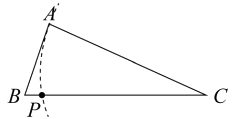 D、
D、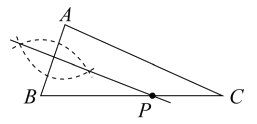 8. 已知=⊙O的直径CD=10cm,AB是⊙O的弦, ,垂足为M,且AB=8cm,则AC的长为( )A、 B、 C、 或 D、 或9. 已知二次函数 的图象如图,分析下列四个结论:① ;② ;③ ;④ .其中正确的结论有( )
8. 已知=⊙O的直径CD=10cm,AB是⊙O的弦, ,垂足为M,且AB=8cm,则AC的长为( )A、 B、 C、 或 D、 或9. 已知二次函数 的图象如图,分析下列四个结论:① ;② ;③ ;④ .其中正确的结论有( )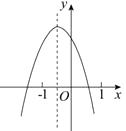 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
10. 函数 中自变量x的取值范围是 .11. 学校射击队计划从甲、乙两人中选拔一人参加运动会射击比赛,在选拔过程中,每人射击10次,计算他们的平均成绩及方差如表,请你根据表中的数据选一人参加比赛,最适合的人选是 .
选手
甲
乙
平均数(环)
9.5
9.5
方差
0.035
0.015
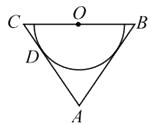
12. 不等式组 的所有整数解的积为13. 若 是关于x的完全平方式,则m= .14. 如图,点 均在坐标轴上,且 , ,若点 的坐标分别为(0,-1),(-2,0),则点 的坐标为 .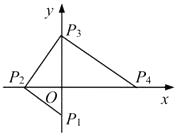 15. 如图,C为半圆内一点,O为圆心,直径AB长为2cm, , ,将 绕圆心O逆时针旋转至 ,点 在OA上,则边BC扫过区域(图中阴影部分)的面积为 .(结果保留 )
15. 如图,C为半圆内一点,O为圆心,直径AB长为2cm, , ,将 绕圆心O逆时针旋转至 ,点 在OA上,则边BC扫过区域(图中阴影部分)的面积为 .(结果保留 )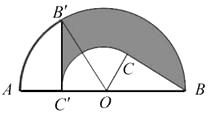 16. 如图,已知直线 与x轴、y轴相交于P、Q两点,与 的图象相交于 、 两点,连接OA、OB.给出下列结论:
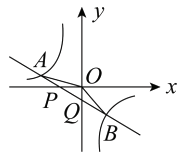
16. 如图,已知直线 与x轴、y轴相交于P、Q两点,与 的图象相交于 、 两点,连接OA、OB.给出下列结论:① ;② ;③ ;④不等式 的解集是 或 .
其中正确结论的序号是 .
 17. 正方形 、 、 、…按如图所示的方式放置.点 、…和点 、…分别在直线 和x轴上,则点 的坐标是 . (n为正整数)
17. 正方形 、 、 、…按如图所示的方式放置.点 、…和点 、…分别在直线 和x轴上,则点 的坐标是 . (n为正整数)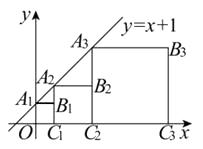
三、解答题
-
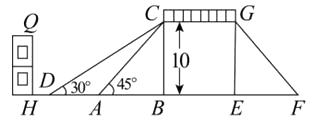
18. 计算: .19. 先化简,再求值: ,其中 .20. 如图是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面AC的倾斜角 ,在距A点10米处有一建筑物HQ.为了方便行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角 ,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).
(参考数据: , )
 21. 如图,在 中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
21. 如图,在 中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF. (1)、求证:AF=DC;
(1)、求证:AF=DC;
(2)、若 ,试判断四边形ADCF的形状,并证明你的结论.22. 某地2015年为做好“精准扶贫”,投入资金1280万元用于异地安置,并规划投入资金逐年增加,2017年在2015年的基础上增加投入资金1600万元.(1)、从2015年到2017年,该地投入异地安置资金的年平均增长率为多少?
(2)、在2017年异地安置的具体实施中,该地计划投入资金不低于500万元用于优先搬迁租房奖励,规定前1000户(含第1000户)每户每天奖励8元,1000户以后每户每天奖励5元,按租房400天计算,求2017年该地至少有多少户享受到优先搬迁租房奖励.
23. 某电视台为了解本地区电视节目的收视情况,对部分市民开展了“你最喜爱的电视节目”的问卷调查(每人只填写一项),根据收集的数据绘制了两幅不完整的统计图(如图所示),根据要求回答下列问题: (1)、本次问卷调查共调查了名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为;
(1)、本次问卷调查共调查了名观众;图②中最喜爱“新闻节目”的人数占调查总人数的百分比为;
(2)、补全图①中的条形统计图;(3)、现有最喜爱“新闻节目”(记为A),“体育节目”(记为B),“综艺节目”(记为C),“科普节目”(记为D)的观众各一名,电视台要从四人中随机抽取两人参加联谊活动,请用列表或画树状图的方法,求出恰好抽到最喜爱“B”和“C”两位观众的概率.