广西贺州市2018年中考数学试卷
试卷更新日期:2018-08-09 类型:中考真卷
一、选择题
-
1. 在﹣1、1、 、2这四个数中,最小的数是( )
A、﹣1 B、1 C、 D、2 -
2. 如图,下列各组角中,互为对顶角的是( )
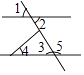 A、∠1和∠2 B、∠1和∠3 C、∠2和∠4 D、∠2和∠5
A、∠1和∠2 B、∠1和∠3 C、∠2和∠4 D、∠2和∠5 -
3. 4的平方根是( )A、2 B、﹣2 C、±2 D、16
-
4. 下列图形中,属于中心对称图形的是( )
A、 B、
B、 C、
C、 D、
D、
-
5. 若一组数据:1、2、x、4、5的众数为5,则这组数据的中位数是( )
A、1 B、2 C、4 D、5 -
6. 下列运算正确的是( )
A、a2•a2=2a2 B、a2+a2=a4 C、(a3)2=a6 D、a8÷a2=a4 -
7. 下列各式分解因式正确的是( )
A、x2+6xy+9y2=(x+3y)2 B、2x2﹣4xy+9y2=(2x﹣3y)2 C、2x2﹣8y2=2(x+4y)(x﹣4y) D、x(x﹣y)+y(y﹣x)=(x﹣y)(x+y) -
8. 如图,这是一个几何体的三视图,根据图中所示数据计算这个几何体的侧面积为( )
 A、9π B、10π C、11π D、12π
A、9π B、10π C、11π D、12π -
9. 如图,在同一平面直角坐标系中,一次函数y1=kx+b(k、b是常数,且k≠0)与反比例函数y2= (c是常数,且c≠0)的图象相交于A(﹣3,﹣2),B(2,3)两点,则不等式y1>y2的解集是( )
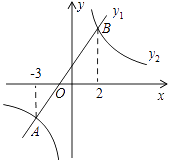 A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<2
A、﹣3<x<2 B、x<﹣3或x>2 C、﹣3<x<0或x>2 D、0<x<2 -
10. 如图,在△ABC中,∠BAC=90°,AD⊥BC,垂足为D,E是边BC的中点,AD=ED=3,则BC的长为( )
 A、3 B、3 C、6 D、6
A、3 B、3 C、6 D、6 -
11. 如图,AB是⊙O的直径,且经过弦CD的中点H,已知sin∠CDB= ,BD=5,则AH的长为( )
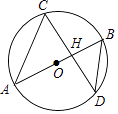 A、 B、 C、 D、
A、 B、 C、 D、 -
12. 如图,正方形ABCD的边长为1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,依此下去,第n个正方形的面积为( )
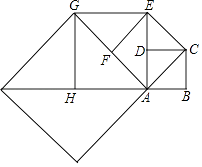 A、( )n﹣1 B、2n﹣1 C、( )n D、2n
A、( )n﹣1 B、2n﹣1 C、( )n D、2n
二、填空题
-
13. 要使二次根式 有意义,则x的取值范围是 .
-
14. 医学家发现了一种病毒,其长度约为0.00000029mm,用科学记数法表 mm.
-
15. 从﹣1、0、 、π、5.1、7这6个数中随机抽取一个数,抽到无理数的概率是 .
-
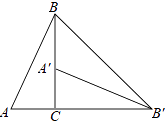
16. 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接BB',若∠A′B′B=20°,则∠A的度数是 .
-
17. 某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30﹣x)件,若使利润最大,则每件商品的售价应为元.
-
18. 如图,正方形ABCD的边长为12,点E在边AB上,BE=8,过点E作EF∥BC,分别交BD、CD于G、F两点.若点P、Q分别为DG、CE的中点,则PQ的长为 .

三、解答题
-
19. 计算:(﹣1)2018+|﹣ |﹣( ﹣π)0﹣2sin60°.
-
20. 解分式方程: +1=
-
21. 某中学为了了解学生每周在校体育锻炼时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时)
频数(人数)
频率
2≤t<3
4
0.1
3≤t<4
10
0.25
4≤t<5
a
0.15
5≤t<6
8
b
6≤t<7
12
0.3
合计
40
1
 (1)、表中的a= , b=;(2)、请将频数分布直方图补全;
(1)、表中的a= , b=;(2)、请将频数分布直方图补全;
(3)、若该校共有1200名学生,试估计全校每周在校参加体育锻炼时间至少有4小时的学生约为多少名?
-
22. 如图,一艘游轮在A处测得北偏东45°的方向上有一灯塔B.游轮以20 海里/时的速度向正东方向航行2小时到达C处,此时测得灯塔B在C处北偏东15°的方向上,求A处与灯塔B相距多少海里?(结果精确到1海里,参考数据: ≈1.41, ≈1.73)

-
23. 某自行车经销商计划投入7.1万元购进100辆A型和30辆B型自行车,其中B型车单价是A型车单价的6倍少60元.
(1)、求A、B两种型号的自行车单价分别是多少元?(2)、后来由于该经销商资金紧张,投入购车的资金不超过5.86万元,但购进这批自行年的总数不变,那么至多能购进B型车多少辆?
-
24. 如图,在△ABC中,∠ACB=90°,O、D分别是边AC、AB的中点,过点C作CE∥AB交DO的延长线于点E,连接AE.
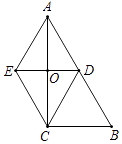 (1)、求证:四边形AECD是菱形;(2)、若四边形AECD的面积为24,tan∠BAC= ,求BC的长.
(1)、求证:四边形AECD是菱形;(2)、若四边形AECD的面积为24,tan∠BAC= ,求BC的长. -
25. 如图,AB是⊙O的弦,过AB的中点E作EC⊥OA,垂足为C,过点B作直线BD交CE的延长线于点D,使得DB=DE.
 (1)、求证:BD是⊙O的切线;(2)、若AB=12,DB=5,求△AOB的面积.
(1)、求证:BD是⊙O的切线;(2)、若AB=12,DB=5,求△AOB的面积. -
26. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c交x轴于A、B两点(A在B的左侧),且OA=3,OB=1,与y轴交于C(0,3),抛物线的顶点坐标为D(﹣1,4).
 (1)、求A、B两点的坐标;(2)、求抛物线的解析式;(3)、过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
(1)、求A、B两点的坐标;(2)、求抛物线的解析式;(3)、过点D作直线DE∥y轴,交x轴于点E,点P是抛物线上B、D两点间的一个动点(点P不与B、D两点重合),PA、PB与直线DE分别交于点F、G,当点P运动时,EF+EG是否为定值?若是,试求出该定值;若不是,请说明理由.
