湖南省怀化市2018年中考数学试卷
试卷更新日期:2018-08-09 类型:中考真卷
一、选择题
-
1. -2018的绝对值是( )A、2018 B、﹣2018 C、 D、±20182. 如图,直线a∥b,∠1=60°,则∠2=( )
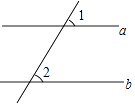 A、30° B、60° C、45° D、120°3. 在国家“一带一路”倡议下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途径城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示为( )
A、30° B、60° C、45° D、120°3. 在国家“一带一路”倡议下,我国与欧洲开通了互利互惠的中欧班列.行程最长,途径城市和国家最多的一趟专列全程长13000km,将13000用科学记数法表示为( )
A、13×103 B、1.3×103 C、13×104 D、1.3×1044. 下列几何体中,其主视图为三角形的是( )
A、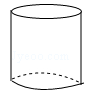 B、
B、 C、
C、 D、
D、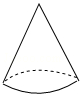 5. 下列说法正确的是( )
5. 下列说法正确的是( )
A、调查舞水河的水质情况,采用抽样调查的方式 B、数据2.0,﹣2,1,3的中位数是﹣2 C、可能性是99%的事件在一次实验中一定会发生 D、从2000名学生中随机抽取100名学生进行调查,样本容量为2000名学生6. 使 有意义的x的取值范围是( )
A、x≤3 B、x<3 C、x≥3 D、x>37. 二元一次方程组 的解是( )A、 B、 C、 D、8. 下列命题是真命题的是( )
A、两直线平行,同位角相等 B、相似三角形的面积比等于相似比 C、菱形的对角线相等 D、相等的两个角是对顶角9. 一艘轮船在静水中的最大航速为30km/h,它以最大航速沿江顺流航行100km所用时间,与以最大航速逆流航行80km所用时间相等,设江水的流速为v km/h,则可列方程为( )
A、 = B、 = C、 = D、 =10. 函数y=kx﹣3与y= (k≠0)在同一坐标系内的图象可能是( )A、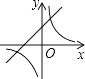 B、
B、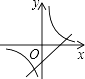 C、
C、 D、
D、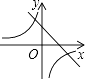
二、填空题
-
11. 因式分解:ab+ac= .
12. 计算:a2•a3= .13. 一个不透明的口袋中有5个完全相同的小球,把它们分别标号为1,2,3,4,5,随机提取一个小球, 则取出的小球标号是奇数的概率是 .14. 关于x的一元二次方程x2+2x+m=0有两个相等的实数根,则m的值是 .15. 一个正多边形的每一个外角都是36°,则这个正多边形的边数是 .
三、解答题
-
16. 计算:2sin30°﹣(π﹣ )0+| ﹣1|+( )﹣117. 解不等式组 ,并把它的解集在数轴上表示出来.
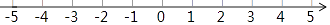 18. 已知:如图,点A.F,E.C在同一直线上,AB∥DC,AB=CD,∠B=∠D.
18. 已知:如图,点A.F,E.C在同一直线上,AB∥DC,AB=CD,∠B=∠D. (1)、求证:△ABE≌△CDF;(2)、若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.19. 某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)、求y与x的函数表达式,其中0≤x≤21;(2)、若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.20. 为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题:
(1)、求证:△ABE≌△CDF;(2)、若点E,G分别为线段FC,FD的中点,连接EG,且EG=5,求AB的长.19. 某学校积极响应怀化市“三城同创”的号召,绿化校园,计划购进A,B两种树苗,共21棵,已知A种树苗每棵90元,B种树苗每棵70元.设购买A种树苗x棵,购买两种树苗所需费用为y元.(1)、求y与x的函数表达式,其中0≤x≤21;(2)、若购买B种树苗的数量少于A种树苗的数量,请给出一种费用最省的方案,并求出该方案所需费用.20. 为弘扬中华传统文化,我市某中学决定根据学生的兴趣爱好组建课外兴趣小组,因此学校随机抽取了部分同学的兴趣爱好进行调查,将收集的数据整理并绘制成下列两幅统计图,请根据图中的信息,完成下列问题: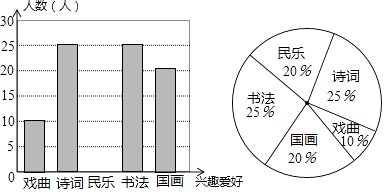 (1)、学校这次调查共抽取了名学生;
(1)、学校这次调查共抽取了名学生;
(2)、补全条形统计图;(3)、在扇形统计图中,“戏曲”所在扇形的圆心角度数为;(4)、设该校共有学生2000名,请你估计该校有多少名学生喜欢书法?21. 已知:如图,AB是⊙O的直径,AB=4,点F,C是⊙O上两点,连接AC,AF,OC,弦AC平分∠FAB,∠BOC=60°,过点C作CD⊥AF交AF的延长线于点D,垂足为点D.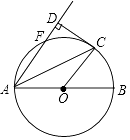 (1)、求扇形OBC的面积(结果保留);(2)、求证:CD是⊙O的切线.22. 已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.
(1)、求扇形OBC的面积(结果保留);(2)、求证:CD是⊙O的切线.22. 已知:如图,在四边形ABCD中,AD∥BC.点E为CD边上一点,AE与BE分别为∠DAB和∠CBA的平分线.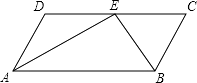 (1)、请你添加一个适当的条件 , 使得四边形ABCD是平行四边形,并证明你的结论;(2)、作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);(3)、在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF= ,求⊙O的半径.23. 如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)、请你添加一个适当的条件 , 使得四边形ABCD是平行四边形,并证明你的结论;(2)、作线段AB的垂直平分线交AB于点O,并以AB为直径作⊙O(要求:尺规作图,保留作图痕迹,不写作法);(3)、在(2)的条件下,⊙O交边AD于点F,连接BF,交AE于点G,若AE=4,sin∠AGF= ,求⊙O的半径.23. 如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.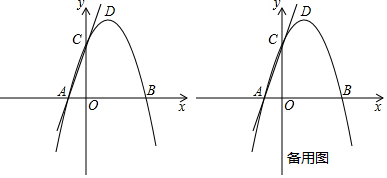 (1)、求抛物线的解析式和直线AC的解析式;(2)、请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)、试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式和直线AC的解析式;(2)、请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;(3)、试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.