四川省马边彝族自治县2018届九年级毕业会考调研检测数学试卷
试卷更新日期:2018-08-07 类型:中考模拟
一、单选题
-
1. 2018的相反数( )A、 2018 B、-2018 C、|-2018| D、2. 将一副三角板按如图方式摆放,∠1与∠2不一定互补的是( )A、
 B、
B、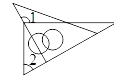 C、
C、 D、
D、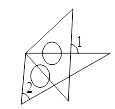 3. 已知某班有40名学生,将他们的身高分成4组,在160~165cm区间的有8名学生,那么这个小组的人数占全体的( )A、10% B、15% C、20% D、25%4. 下列变形中不正确的是 ( )A、若a>b,则ac2>bc2 (c为有理数) B、由 得 C、由 得 D、由 得5. 二次函数y=2x2-8x+m满足以下条件:当-2<x<-1时,它的图像位于x轴的下方;当6<x<7时,它的图像位于x轴的上方,则m的值为( ).A、8 B、-10 C、-42 D、-246. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°7. 九年级某班的部分同学去植树,若每人平均植树7棵,则还剩9棵;若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设同学人数为x人,则下列能准确求出同学人数与植树总棵数的是 ( )
3. 已知某班有40名学生,将他们的身高分成4组,在160~165cm区间的有8名学生,那么这个小组的人数占全体的( )A、10% B、15% C、20% D、25%4. 下列变形中不正确的是 ( )A、若a>b,则ac2>bc2 (c为有理数) B、由 得 C、由 得 D、由 得5. 二次函数y=2x2-8x+m满足以下条件:当-2<x<-1时,它的图像位于x轴的下方;当6<x<7时,它的图像位于x轴的上方,则m的值为( ).A、8 B、-10 C、-42 D、-246. 当A为锐角,且<cosA<时,∠A的范围是( )A、0°<∠A<30° B、30°<∠A<60° C、60°<∠A<90° D、30°<∠A<45°7. 九年级某班的部分同学去植树,若每人平均植树7棵,则还剩9棵;若每人平均植树9棵,则有1名同学植树的棵数不到8棵.若设同学人数为x人,则下列能准确求出同学人数与植树总棵数的是 ( )
A、7x+9-9(x-1)>0 B、7x+9-9(x-1)<8 C、 D、8. 如图,抛物线y=ax2+bx+c(a>0)过点(1,0)和点(0,-2),且顶点在第三象限,设P=a-b+c,则P的取值范围是( ) A、-1<P<0 B、-2<P<0 C、-4<P<-2 D、-4<P<09. 如图,直线 与双曲线 (k>0,x>0)交于点A,将直线 向上平移4个单位长度后,与y轴交于点C,与双曲线 (k>0,x>0)交于点B,若OA=3BC,则k的值为( )
A、-1<P<0 B、-2<P<0 C、-4<P<-2 D、-4<P<09. 如图,直线 与双曲线 (k>0,x>0)交于点A,将直线 向上平移4个单位长度后,与y轴交于点C,与双曲线 (k>0,x>0)交于点B,若OA=3BC,则k的值为( ) A、 B、 C、6 D、310. 如图,直线 ∥ ∥ ,直线AC分别交 , , 于点A,B,C;直线DF分别交 , , 于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( )
A、 B、 C、6 D、310. 如图,直线 ∥ ∥ ,直线AC分别交 , , 于点A,B,C;直线DF分别交 , , 于点D,E,F.AC与DF相交于点G,且AG=2,GB=1,BC=5,则 的值为( ) A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
11. 的倒数是 .12. 当x=2时,二次根式 的值是13. 某学生7门学科考试成绩的平均分是80分,其中 门学科都考了78分,则另外4门学科成绩的平均分是.
14. 如图,在Rt△ABC中,∠ACB=90°,AC BC=2,以BC为直径的半圆交AB于点D,P是弧CD上的一个动点,连结AP,则AP的最小值是 15. 已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为( , 0 ),⊙M的切线OC与直线AB交于点C.则∠ACO=.
15. 已知,如图,半径为1的⊙M经过直角坐标系的原点O,且与x轴、y轴分别交于点A、B,点A的坐标为( , 0 ),⊙M的切线OC与直线AB交于点C.则∠ACO=. 16. 如图,点A(m,6),B(n,1)在反比例函数 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是 .
16. 如图,点A(m,6),B(n,1)在反比例函数 的图象上,AD⊥x轴于点D,BC⊥x轴于点C,点E在CD上,CD=5,△ABE的面积为10,则点E的坐标是 .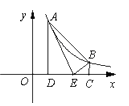
三、解答题
-
17. 计算:18. 若不等式组 的解集为x>3,求a的取值范围.
19. 先化简,再求值: ,其中 .20. 如图,在 Rt△ABC,∠ACB=90°,AC=BC,分别过A、B作直线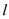 的垂线,垂足分别为M、N.
的垂线,垂足分别为M、N.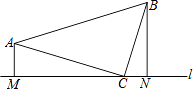 (1)、求证:△AMC≌△CNB;(2)、若AM=3,BN=5,求AB的长.21. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的 5 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
(1)、求证:△AMC≌△CNB;(2)、若AM=3,BN=5,求AB的长.21. 某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的 5 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: (1)、这次调查的学生共有多少名?
(1)、这次调查的学生共有多少名?
(2)、请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)、如果要在这 5 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
22. 某服装店用3.6万元购进A、B两种品牌的服装,销售完后共获利0.6万元,其进价和售价如下表: (1)、该商场购进A、B两种服装各多少件?(2)、第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于8160元,则B种服装最低打几折销售?
(1)、该商场购进A、B两种服装各多少件?(2)、第二次以原价购进A、B两种服装,购进B服装的件数不变,购进A服装的件数是第一次的2倍,A种服装按原价出售,而B种服装打折销售;若两种服装销售完毕,要使第二次销售活动获利不少于8160元,则B种服装最低打几折销售?
23. 如图,O是△ABC的内心,BO的延长线和△ABC的外接圆相交于D,连结DC、DA、OA、OC,四边形OADC为平行四边形.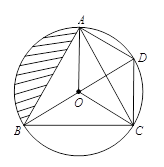 (1)、求证:△BOC≌△CDA.(2)、若AB=2,求阴影部分的面积.24. 已知:关于x 的一元二次方程:(m-1)x2+(m-2)x-1=0(m为实数).
(1)、求证:△BOC≌△CDA.(2)、若AB=2,求阴影部分的面积.24. 已知:关于x 的一元二次方程:(m-1)x2+(m-2)x-1=0(m为实数).
(1)、若方程有两个不相等的实数根,求m的取值范围;(2)、若 是此方程的实数根,抛物线y=(m-1)x2+(m-2)x-1与x轴交于A、B,抛物线的顶点为C,求△ABC的面积.25. 如图,在△ABC中,AB AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F.
AC,AE是∠BAC的平分线,∠ABC的平分线BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交AB于点F. (1)、求证:AE为⊙O的切线;(2)、当BC=4,AC=6时,求⊙O的半径;
(1)、求证:AE为⊙O的切线;(2)、当BC=4,AC=6时,求⊙O的半径;
(3)、在(2)的条件下,求线段BG的长.
26. 如图,抛物线 过点 , . 为线段OA上一个动点(点M与点A不重合),过点M作垂直于x轴的直线与直线AB和抛物线分别交于点P、N. (1)、求直线AB的解析式和抛物线的解析式;(2)、如果点P是MN的中点,那么求此时点N的坐标;(3)、如果以B,P,N为顶点的三角形与 相似,求点M的坐标.
(1)、求直线AB的解析式和抛物线的解析式;(2)、如果点P是MN的中点,那么求此时点N的坐标;(3)、如果以B,P,N为顶点的三角形与 相似,求点M的坐标.