四川省泸州市泸县2018届九年级数学中考模拟试卷(六)
试卷更新日期:2018-08-07 类型:中考模拟
一、单选题
-
1. 如果a与﹣3互为倒数,那么a是( )A、﹣3 B、 C、3 D、2. 据报道,目前我国“天河二号”超级计算机的运算速度位居全球第一,其运算速度达到了每秒338 600 000亿次,数字338 600 000用科学记数法可简洁表示为( )A、3.386×108 B、0.3386×109 C、33.86×107 D、3.386×1093. 一个等腰三角形的两边长分别为2和5,则它的周长为( )A、7 B、9 C、12 D、9或124. 某班七个兴趣小组人数分别为4,4,5,5,x,6,7,已知这组数据的平均数是5,则这组数据的众数和中位数分别是( )A、4,5 B、4,4 C、5,4 D、5,55. 六边形的内角和为( )A、360° B、540° C、720° D、900°6. 如图是由三个相同小正方体组成的几何体的主视图,那么这个几何体可以是( )
 A、
A、 B、
B、 C、
C、 D、
D、 7. 函数y= 中,自变量x的取值范围在数轴上表示正确的是( )A、
7. 函数y= 中,自变量x的取值范围在数轴上表示正确的是( )A、 B、
B、 C、
C、 D、
D、 8. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根9. 如图,在▱ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2 , 则S△AOB等于( )
8. 关于x的一元二次方程x2+ax﹣1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根9. 如图,在▱ABCD中,E为CD的中点,AE交BD于点O,S△DOE=12cm2 , 则S△AOB等于( ) A、24cm2 B、36cm2 C、48cm2 D、60cm210. 一枚质地均匀的骰子,其六个面上分别标有数字1,2,3,4,5,6,投掷一次,朝上一面的数字是偶数的概率为( )A、 B、 C、 D、11. 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )
A、24cm2 B、36cm2 C、48cm2 D、60cm210. 一枚质地均匀的骰子,其六个面上分别标有数字1,2,3,4,5,6,投掷一次,朝上一面的数字是偶数的概率为( )A、 B、 C、 D、11. 如图,AB为⊙O的直径,点C在⊙O上,若∠OCA=50°,AB=4,则 的长为( )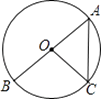 A、 π B、 π C、 π D、 π
A、 π B、 π C、 π D、 π二、填空题
-
12. 分解因式:2m2-8= .13. 矩形ABCD的对角线AC,BD相交于点O,若AB=AO,则∠ABD的度数是 .
14. 设x1 , x2是一元二次方程x2﹣2x﹣3=0的两根,则x12+x22= .
15. 如图,在△ABC中,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE,BE分别交于点G、H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC•AD= AE2;④S△ABC=2S△ADF . 其中正确结论的序号是 . (把你认为正确结论的序号都填上)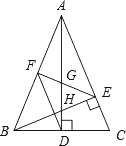
三、解答题
-
16. 计算: ﹣4cos45°﹣(π﹣3.14)0 .17. 已知:如图,点E,C在线段BF上,AB=DE,AC=DF,BE=CF.求证:AB∥DE.
 18. 先化简,再求值:( )÷ ,其中x= +1.19. 学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).
18. 先化简,再求值:( )÷ ,其中x= +1.19. 学校实施新课程改革以来,学生的学习能力有了很大提高.王老师为进一步了解本班学生自主学习、合作交流的现状,对该班部分学生进行调查,把调查结果分成四类(A:特别好,B:好,C:一般,D:较差)后,再将调查结果绘制成两幅不完整的统计图(如图).请根据统计图解答下列问题:
 (1)、本次调查中,王老师一共调查了名学生;(2)、将条形统计图补充完整;(3)、为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
(1)、本次调查中,王老师一共调查了名学生;(2)、将条形统计图补充完整;(3)、为了共同进步,王老师从被调查的A类和D类学生中分别选取一名学生进行“兵教兵”互助学习,请用列表或画树状图的方法求出恰好选中一名男生和一名女生的概率.
20. 学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)、求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)、学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
21. 如图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75) 22. 如图,一次函数y=﹣x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A(1,a),B两点.
22. 如图,一次函数y=﹣x+4的图象与反比例函数y= (k为常数,且k≠0)的图象交于A(1,a),B两点.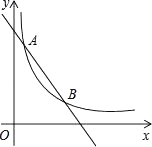 (1)、求反比例函数的表达式及点B的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
(1)、求反比例函数的表达式及点B的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
23. 如图,AB是⊙O的直径,D、E为⊙O上位于AB异侧的两点,连接BD并延长至点C,使得CD=BD,连接AC交⊙O于点F,连接AE、DE、DF.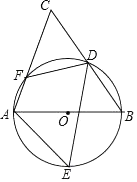 (1)、求证:∠E=∠C;(2)、若DF=6cm,cosB= ,E是弧AB的中点,求DE的长.
(1)、求证:∠E=∠C;(2)、若DF=6cm,cosB= ,E是弧AB的中点,求DE的长.
24. 如图,在平面直角坐标系xOy中,O为原点,▱ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(﹣2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点. (1)、求抛物线的解析式;(2)、求证:DE是⊙P的切线;(3)、若将△CDE绕点D顺时针旋转90°,点E的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由;(4)、若点M为此抛物线的顶点,平面上是否存在点N,使得以点B、D、M、N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、求证:DE是⊙P的切线;(3)、若将△CDE绕点D顺时针旋转90°,点E的对应点E′会落在抛物线y=ax2+bx+c上吗?请说明理由;(4)、若点M为此抛物线的顶点,平面上是否存在点N,使得以点B、D、M、N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.