四川省乐山市井研县2018届九年级数学中考模拟试卷

试卷更新日期：2018-08-07 类型：中考模拟

进入出卷网下载

一、单选题

1. 《九章算术》中注有“今两算得失相反，要令正负以名之”，意思是：今有两数若其意义相反，则分别叫做正数与负数，若气温为零上10℃记作+10℃，则﹣3℃表示气温为（）

A、零上3℃ B、零下3℃ C、零上7℃ D、零下7℃

查看试题解析
2. 下列各式计算正确的是（）

A、 $4 a - a = 3$ B、 $a^{8} \div a^{2} = a^{4}$ C、 ${(- a^{3})}^{2} = a^{6}$ D、 $a^{2} \cdot a^{3} = a^{6}$

查看试题解析
3. 如图是按1：10的比例画出的一个几何体的三视图，则该几何体的侧面积是（）

A、 $200$ B、 $600$ C、 $100$ D、 $200 π$

查看试题解析
4. 一组数据4，5，6，4，4，7， $x$ ，5的平均数是5.5，则该组数据的中位数和众数分别是（）

A、4，4 B、5，4 C、5，6 D、6，7

查看试题解析
5. 如图，在平面直角坐标系中，∠α的一边与 $x$ 轴正半轴重合，顶点为坐标原点，另一边过点 $A (1 ， 2)$ ，那么sinα的值为（）

A、 $\frac{2 \sqrt{5}}{5}$ B、 $\frac{1}{2}$ C、 $2$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
6. 已知关于x的方程2x-a=x-1的解是非负数，则a的取值范围为（）

A、 $a \geq 1$ B、 $a > 1$ C、 $a \leq 1$ D、 $a < 1$

查看试题解析
7. 如图，四边形ABCD内接于⊙O，延长CO交圆于点E，连接BE.若∠A=100°，∠E=60°，则∠OCD的度数为（）

A、30° B、50° C、60° D、80°

查看试题解析
8. 如图，△ABC的面积是12，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG的面积是（）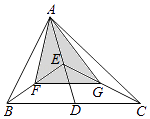

A、4.5 B、5 C、5.5 D、6

查看试题解析
9. 若关于x的一元二次方程 $(x - 2) (x - 3) = m$ 有实数根 $x_{1} ， x_{2}$ ，且 $x_{1} \neq x_{2}$ ，有下列结论：① $x_{1} = 2 ， x_{2} = 3$ ；② $m > - \frac{1}{4}$ ；③二次函数 $y = (x - x_{1}) (x - x_{2}) + m$ 的图象与x轴的交点坐标分别为（2，0）和（3，0）.其中正确的个数有（）

A、0 B、1 C、2 D、3

查看试题解析
10. 如图，M是双曲线 $y = \frac{\sqrt{3}}{x}$ 上一点，过点M作 $x$ 轴、y轴的垂线，分别交直线 $y = - x + m$ 于点D，C，若直线 $y = - x + m$ 与 $y$ 轴交于点A，与轴交于点B，则 $A D \cdot B C$ 的值为（）

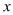A、 $\sqrt{2}$ B、 $\sqrt{3}$ C、 $\sqrt{6}$ D、 $2 \sqrt{3}$

查看试题解析

二、填空题

11. -7的倒数是

查看试题解析
12. 小明和他的爸爸、妈妈共3人站成一排拍照，他的爸爸、妈妈相邻的概率是

查看试题解析
13. 分解因式： ${(y + 2 x)}^{2} - {(x + 2 y)}^{2}$ =

查看试题解析
14. 如图，扇形纸片AOB中，已知∠AOB=90º，OA=6，取OA的中点C，过点C作DC⊥OA交 $\overset{⌢}{A B}$ 于点D，点F是 $\overset{⌢}{A B}$ 上一点.若将扇形BOD沿OD翻折，点B恰好与点F重合，用剪刀沿着线段BD、DF、FA依次剪下，则剩下的纸片（阴影部分）面积是

查看试题解析
15. 圆锥的底面直径为40cm，母线长90cm则它的侧面展开图的圆心角度数为

查看试题解析
16. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0$ 有两个实数根，且其中一个根为另一个根的2倍，则称这样的方程为“倍根方程”．以下关于倍根方程的说法，正确的是（写出所有正确说法的序号）．
①方程 $x^{2} - x - 2 = 0$ 是倍根方程；②若 $(x - 2) (m x + n) = 0$ 是倍根方程，则 $4 m^{2} + 5 m n + n^{2} = 0$ ；③若点 $(p ， q)$ 在反比例函数 $y = \frac{2}{x}$ 的图像上，则关于 $x$ 的方程 $p x^{2} + 3 x + q = 0$ 是倍根方程；④若方程 $a x^{2} + b x + c = 0$ 是倍根方程，且相异两点 $M (1 + t ， s)$ ， $N (4 - t ， s)$ 都在抛物线 $y = a x^{2} + b x + c$ 上，则方程 $a x^{2} + b x + c = 0$ 的一个根为 $\frac{5}{4}$ ．

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{2})}^{- 1} - | - \sqrt{3} | + \sqrt{12} + {(1 - π)}^{0}$

查看试题解析
18. 解不等式组 ${\begin{matrix} x - 3 (x - 2) \geq 4 \\ \frac{2 x - 1}{5} < \frac{x + 1}{2} \end{matrix}$ ，并把解集在数轴上表示出来.

查看试题解析
19. 已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M作ME⊥CD于点E，∠1=∠2．

(1)、若CE=1，求BC的长；

(2)、求证：AM=DF+ME．

查看试题解析
20. 当m、n为何值时，方程组 ${\begin{matrix} m x + y = n \\ 2 x - y = 7 \end{matrix}$ 与方程组 ${\begin{matrix} x + n y = m \\ 3 x + y = 8 \end{matrix}$ 同解？

查看试题解析
21. 某校初三（1）班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动，收集整理数据后，老师将减压方式分为五类，并绘制了图1、图2两个不完整的统计图，请根据图中的信息解答下列问题．

(1)、初三（1）班接受调查的同学共有多少名；

(2)、补全条形统计图，并计算扇形统计图中的“体育活动C”所对应的圆心角度数；

(3)、若喜欢“交流谈心”的5名同学中有三名男生和两名女生；老师想从5名同学中任选两名同学进行交流，直接写出选取的两名同学都是女生的概率．

查看试题解析
22. 如图，为了开发利用海洋资源，某勘测飞机预测量一岛屿两端A、B的距离，飞机在距海平面垂直高度为100米的点C处测得端点A的俯角为60°，然后沿着平行于AB的方向水平飞行了500米，在点D测得端点B的俯角为45°，求岛屿两端A、B的距离.

查看试题解析
23. 已知一次函数 $y = \frac{2}{3} x + b$ 的图象分别与坐标轴相交于A、B两点（如图所示），与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象相交于点C，OA=3.

(1)、求一次函数的解析式和点B的坐标；

(2)、作CD⊥x轴，垂足为D，若 $S_{△ A O B} ： S_{梯形 B O D C}$ =1：3，求反比例函数 $y = \frac{k}{x}$ 的解析式.

查看试题解析
24. 已知 $x_{1} ， x_{2}$ 是关于x的一元二次方程 $4 k x^{2} - 4 k x + k + 1 = 0$ 的两个实数根.

(1)、是否存在实数k，使 $(2 x_{1} - x_{2}) (x_{1} - 2 x_{2}) = - \frac{3}{2}$ 成立？若存在，求出k的值；若不存在，请说明理由.

(2)、求使 $\frac{x_{1}}{x_{2}} + \frac{x_{2}}{x_{1}} - 2$ 的值为整数的实数k的整数值.

查看试题解析
25.

(1)、【探索发现】
如图①，是一张直角三角形纸片，∠B=90°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为．

(2)、【拓展应用】
如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为．（用含a，h的代数式表示）

(3)、【灵活应用】
如图③，有一块“缺角矩形”ABCDE，AB=32，BC=40，AE=20，CD=16，小明从中剪出了一个面积最大的矩形（∠B为所剪出矩形的内角），求该矩形的面积．

(4)、【实际应用】
如图④，现有一块四边形的木板余料ABCD，经测量AB=50cm，BC=108cm，CD=60cm，且tanB=tanC= $\frac{4}{3}$ ，木匠徐师傅从这块余料中裁出了顶点M、N在边BC上且面积最大的矩形PQMN，求该矩形的面积．

查看试题解析
26. 如图，二次函数 $y = a x^{2} + b x + c$ 的图象关于y轴对称且交y轴负半轴于点C，与x轴交于点A、B，已知AB=6，OC=4，⊙C的半径为 $\sqrt{5}$ ，P为⊙C上一动点．

(1)、求出二次函数的解析式；

(2)、是否存在点P，使得△PBC为直角三角形？若存在，求出点P的坐标；若不存在，请说明理由；

(3)、连接PB，若E为PB的中点，连接OE，则OE的最大值是多少？

查看试题解析