四川省广元市利州区2018届九年级数学中考一模试卷

试卷更新日期：2018-08-07 类型：中考模拟

进入出卷网下载

一、单选题

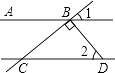
1. $- \frac{1}{4}$ 的绝对值是（）

A、﹣4 B、 $\frac{1}{4}$ C、4 D、0.4

查看试题解析
2. 下列运算正确的是（　　）

A、a³+a⁴=a⁷ B、（2a⁴）³=8a⁷ C、2a³•a⁴=2a⁷ D、a⁸÷a²=a⁴

查看试题解析
3. 如图，AB∥CD，DB⊥BC，∠1=40°，则∠2的度数是（）

A、40° B、50° C、60° D、140°

查看试题解析
4. 如图，网格中的四个格点组成菱形ABCD，则tan∠DBC的值为（）

A、 $\frac{1}{3}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、3

查看试题解析
5. 如图，在△ABC中，AB＝AC＝13，BC＝10，点D为BC的中点，DE⊥AB，垂足为点E，则DE的长为（）

A、 $\frac{10}{13}$ B、 $\frac{15}{13}$ C、 $\frac{60}{13}$ D、 $\frac{75}{13}$

查看试题解析
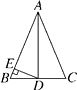6. 某服装厂准备加工400套运动装，在加工完160套后，采用了新技术，使得工作效率比原计划提高了20%，结果共用了18天完成任务，问计划每天加工服装多少套？在这个问题中，设计划每天加工x套服装，则根据题意可得方程为（）

A、 $\frac{160}{x}$ + $\frac{400 - 160}{(1 + 20 %) x}$ =18 B、 $\frac{160}{x}$ + $\frac{400}{(1 + 20 %) x}$ =18 C、 $\frac{160}{x}$ + $\frac{400 - 160}{20 % x}$ =18 D、 $\frac{400}{x}$ + $\frac{400 - 160}{(1 + 20 %) x}$ =18

查看试题解析
7.
如图，⊙O的直径CD过弦EF的中点G，∠EOD=40°，则∠DCF等于（）

A、80° B、50° C、40° D、20°

查看试题解析
8. 如图，在平行四边形ABCD中，∠C=120°，AD=2AB=4，点H、G分别是边CD、BC上的动点．连接AH、HG，点E为AH的中点，点F为GH的中点，连接EF，则EF的最大值与最小值的差为（）

A、1 B、 $\sqrt{3}$ ﹣1 C、 $\frac{\sqrt{3}}{2}$ D、2﹣ $\sqrt{3}$

查看试题解析
9. 函数y= ${\begin{matrix} x + 1 (x < 1) \\ \frac{2}{x} (x \geq 1) \end{matrix}$ ，当y=a时，对应的x有唯一确定的值，则a的取值范围为（）

A、a≤0 B、a＜0 C、0＜a＜2 D、a≤0或a=2

查看试题解析

二、填空题

10. 分解因式：ax²﹣2a²x+a³= ．

查看试题解析
11. 计算：（ $\sqrt{3}$ +1）（3﹣ $\sqrt{3}$ ）= ．

查看试题解析
12. 如图，直线y=k₁x+b与双曲线y= $\frac{k_{2}}{x}$ 交于A、B两点，其横坐标分别为1和5，则不等式k₁x＜ $\frac{k_{2}}{x}$ +b的解集是．

查看试题解析
13. 如图，∠XOY=45°，一把直角三角尺△ABC的两个顶点A、B分别在OX，OY上移动，其中AB=10，那么点O到顶点A的距离的最大值为．

查看试题解析
14. 如图，⊙P的半径为5，A、B是圆上任意两点，且AB=6，以AB为边作正方形ABCD（点D、P在直线AB两侧）．若AB边绕点P旋转一周，则CD边扫过的面积为．

查看试题解析

三、解答题

15. （﹣ $\frac{1}{2}$ ）^﹣2﹣（2018﹣π）⁰﹣| $\sqrt{3} - 2$ |+2sin60°

查看试题解析
16. 四川省第十三届运动会将于2018年8月在我市举行，某校组织了主题“我是运动会志愿者”的电子小报作品征集活动，先从中随机抽取了部分作品，按A，B，C，D四个等级评分，然后根据统计结果绘制了如下两幅不完整的统计图，请根据图中的信息，解答下列问题：

(1)、求此次抽取的作品中等级为B的作品数，并补全条形统计图；

(2)、求扇形统计图为D的扇形圆心角的度数；

(3)、该校计划从抽取的这些作品中选取部分作品参加市区的作品展．已知其中所选的到市区参展的A作品比B作品少4份，且A、B两类作品数量和正好是本次抽取的四个等级作品数量的 $\frac{1}{5}$ ，求选取到市区参展的B类作品有多少份．

查看试题解析
17. 如图，已知点D在△ABC的BC边上，DE∥AC交AB于E，DF∥AB交AC于F．

(1)、求证：AE=DF；

(2)、若AD平分∠BAC，试判断四边形AEDF的形状，并说明理由．

查看试题解析
18. 如图，在航线l的两侧分别有观测点A和B，点B到航线l的距离BD为4km，点A位于点B北偏西60°方向且与B相距20km处．现有一艘轮船从位于点A南偏东74°方向的C处，沿该航线自东向西航行至观测点A的正南方向E处．求这艘轮船的航行路程CE的长度．（结果精确到0.1km）（参考数据： $\sqrt{3}$ ≈1.73，sin74°≈0.96，cos74°≈0.28，tan74°≈3.49）

查看试题解析
19. 市园林处为了对一段公路进行绿化，计划购买A，B两种风景树共900棵．A， B两种树的相关信息如表：
品种项目
单价（元/棵）
成活率
A
80
92%
B
100
98%
若购买A种树x棵，购树所需的总费用为y元．

(1)、求y与x之间的函数关系式．

(2)、若希望这批树的成活率不低于94%，且使购树的总费用最低，应选购A、B两种树各多少棵？此时最低费用为多少？

查看试题解析
20. 现有一项资助贫困生的公益活动由你来主持，每位参与者需交赞助费5元，活动规则如下：如图是两个可以自由转动的转盘，每个转盘被分成6个相等的扇形，参与者转动这两个转盘，转盘停止后，指针各自指向一个数字，（若指针在分格线上，则重转一次，直到指针指向某一数字为止），若指针最后所指的数字之和为12，则获得一等奖，奖金20元；数字之和为9，则获得二等奖，奖金10元；数字之和为7，则获得三等奖，奖金为5元；其余均不得奖；此次活动所集到的赞助费除支付获奖人员的奖金外，其余全部用于资助贫困生的学习和生活；

(1)、分别求出此次活动中获得一等奖、二等奖、三等奖的概率；

(2)、若此次活动有2000人参加，活动结束后至少有多少赞助费用于资助贫困生？

查看试题解析
21. 如图所示，以Rt△ABC的直角边AB为直径作圆O，与斜边交于点D，E为BC边上的中点，连接DE．

(1)、求证：DE是⊙O的切线；

(2)、连接OE，AE，当∠CAB为何值时，四边形AOED是平行四边形？并在此条件下求sin∠CAE的值．

查看试题解析
22. 如图，二次函数y= $\frac{1}{2} x^{2}$ +bx+c的图象交x轴于A、D两点，并经过B点，已知A点坐标是（2，0），B点的坐标是（8，6）．

(1)、求二次函数的解析式；

(2)、求函数图象的顶点坐标及D点的坐标；

(3)、该二次函数的对称轴交x轴于C点，连接BC，并延长BC交抛物线于E点，连接BD、DE，求△BDE的面积．

查看试题解析
23. 已知△ABC，以AC为边在△ABC外作等腰△ACD，其中AC=AD．

(1)、如图1，若∠DAC=2∠ABC，AC=BC，四边形ABCD是平行四边形，则∠ABC=；

(2)、如图2，若∠ABC=30°，△ACD是等边三角形，AB=3，BC=4．求BD的长；

(3)、如图3，若∠ABC=30°，∠ACD=45°，AC=2，B、D之间距离是否有最大值？如有求出最大值；若不存在，说明理由．

查看试题解析

品种项目	单价（元/棵）	成活率
A	80	92%
B	100	98%