四川省资阳市2018年中考数学试卷

试卷更新日期：2018-08-07 类型：中考真卷

进入出卷网下载

一、选择题

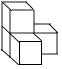
1. ﹣ $\frac{1}{3}$ 的相反数是（）

A、3 B、﹣3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 如图是由四个相同的小正方体堆成的物体，它的正视图是（）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、a²+a³=a⁵ B、a²×a³=a⁶ C、（a+b）²=a²+b² D、（a²）³=a⁶

查看试题解析
4. 下列图形具有两条对称轴的是（）

A、等边三角形 B、平行四边形 C、矩形 D、正方形

查看试题解析
5. ﹣0.00035用科学记数法表示为（）

A、﹣3.5×10^﹣4 B、﹣3.5×10⁴ C、3.5×10^﹣4 D、﹣3.5×10^﹣3

查看试题解析
6. 某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核（考核的满分均为100分），三个方面的重要性之比依次为3：5：2．小王经过考核后所得的分数依次为90、88、83分，那么小王的最后得分是（）

A、87 B、87.5 C、87.6 D、88

查看试题解析
7. 如图，ABCDEF为⊙O的内接正六边形，AB=a，则图中阴影部分的面积是（）

A、 $\frac{π}{6} a^{2}$ B、（ $\frac{π}{6} - \frac{\sqrt{3}}{4}$ ）a² C、 $\frac{\sqrt{3}}{4} a$ ² D、（ $\frac{π}{3} - \frac{\sqrt{3}}{4}$ ）a²

查看试题解析
8. 如图，将矩形ABCD的四个角向内翻折后，恰好拼成一个无缝隙无重叠的四边形EFGH，EH=12厘米，EF=16厘米，则边AD的长是（）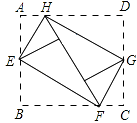

A、12厘米 B、16厘米 C、20厘米 D、28厘米

查看试题解析
9. 已知直线y₁=kx+1（k＜0）与直线y₂=mx（m＞0）的交点坐标为（ $\frac{1}{2}$ ， $\frac{1}{2}$ m），则不等式组mx﹣2＜kx+1＜mx的解集为（）

A、x $> \frac{1}{2}$ B、 $\frac{1}{2} < x < \frac{3}{2}$ C、x $\frac{3}{2}$ D、0 $< x < \frac{3}{2}$

查看试题解析
10. 已知二次函数y=ax²+bx+c的图象如图所示，OA=OC，则由抛物线的特征写出如下含有a、b、c三个字母的等式或不等式：① $\frac{4 a c - b^{2}}{4 a}$ =﹣1；②ac+b+1=0；③abc＞0；④a﹣b+c＞0．其中正确的个数是（）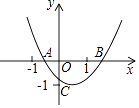

A、4个 B、3个 C、2个 D、1个

查看试题解析

二、填空题

11. 函数y= $\sqrt{x - 1}$ 的自变量x的取值范围是．

查看试题解析
12. 已知a、b满足（a﹣1）²+ $\sqrt{b + 2}$ =0，则a+b= ．

查看试题解析
13. 一口袋中装有若干红色和白色两种小球，这些小球除颜色外没有任何区别，袋中小球已搅匀，蒙上眼睛从中取出一个白球的概率为 $\frac{1}{5}$ ．若袋中白球有4个，则红球的个数是个

查看试题解析
14. 已知：如图，△ABC的面积为12，点D、E分别是边AB、AC的中点，则四边形BCED的面积为．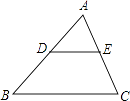

查看试题解析
15. 已知关于x的一元二次方程mx²+5x+m²﹣2m=0有一个根为0，则m= ．

查看试题解析
16. 如图，在平面直角坐标系中，等腰直角三角形OAA₁的直角边OA在x轴上，点A₁在第一象限，且OA=1，以点A₁为直角顶点，OA₁为一直角边作等腰直角三角形OA₁A₂ ，再以点A₂为直角顶点，OA₂为直角边作等腰直角三角形OA₂A₃…依此规律，则点A₂₀₁₈的坐标是．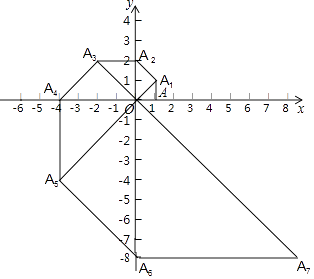

查看试题解析

三、解答题

17. 先化简，再求值： $\frac{a^{2} - b^{2}}{b}$ ÷（ $\frac{a^{2}}{b}$ ﹣a），其中a= $\sqrt{2}$ ﹣1，b=1．

查看试题解析
18. 某茶农要对1号、2号、3号、4号四个品种共500株茶树幼苗进行成活实验，从中选出成活率高的品种进行推广，通过实验得知，3号茶树幼苗成活率为89.6%，把实验数据绘制成图1和图2所示的两幅不完整的统计图．

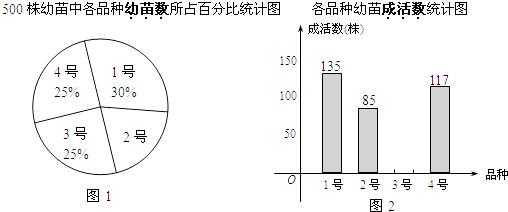(1)、实验所用的2号茶树幼苗的数量是株；

(2)、求出3号茶树幼苗的成活数，并补全统计图2；

(3)、该茶农要从这四种茶树中选择两个品种进行推广，请用列表或画树状图的方法求出1号品种被选中的概率．

查看试题解析
19. 如图，在平面直角坐标系中，直线y₁=2x﹣2与双曲线y₂= $\frac{k}{x}$ 交于A、C两点，AB⊥OA交x轴于点B，且OA=AB．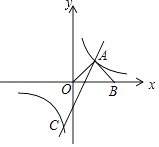

(1)、求双曲线的解析式；

(2)、求点C的坐标，并直接写出y₁＜y₂时x的取值范围．

查看试题解析
20. 为了美化市容市貌，政府决定将城区旁边一块162亩的荒地改建为湿地公园，规划公园分为绿化区和休闲区两部分．

(1)、若休闲区面积是绿化区面积的20%，求改建后的绿化区和休闲区各有多少亩？

(2)、经预算，绿化区的改建费用平均每亩35000元，休闲区的改建费用平均每亩25000元，政府计划投入资金不超过550万元，那么绿化区的面积最多可以达到多少亩？

查看试题解析
21. 已知：如图，在△ABC中，AB=AC，点P是底边BC上一点且满足PA=PB，⊙O是△PAB的外接圆，过点P作PD∥AB交AC于点D．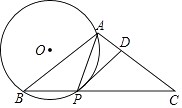

(1)、求证：PD是⊙O的切线；

(2)、若BC=8，tan∠ABC= $\frac{\sqrt{2}}{2}$ ，求⊙O的半径．

查看试题解析
22. 如图是小红在一次放风筝活动中某时段的示意图，她在A处时的风筝线（整个过程中风筝线近似地看作直线）与水平线构成30°角，线段AA₁表示小红身高1.5米．

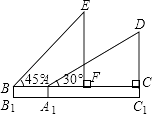(1)、当风筝的水平距离AC=18米时，求此时风筝线AD的长度；

(2)、当她从点A跑动9 $\sqrt{2}$ 米到达点B处时，风筝线与水平线构成45°角，此时风筝到达点E处，风筝的水平移动距离CF=10 $\sqrt{3}$ 米，这一过程中风筝线的长度保持不变，求风筝原来的高度C₁D．

查看试题解析
23. 已知：如图，在Rt△ABC中，∠ACB=90°，点M是斜边AB的中点，MD∥BC，且MD=CM，DE⊥AB于点E，连结AD、CD．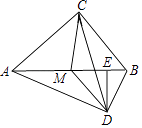

(1)、求证：△MED∽△BCA；

(2)、求证：△AMD≌△CMD；

(3)、设△MDE的面积为S₁ ，四边形BCMD的面积为S₂ ，当S₂= $\frac{17}{5}$ S₁时，求cos∠ABC的值．

查看试题解析
24. 已知：如图，抛物线y=ax²+bx+c与坐标轴分别交于点A（0，6），B（6，0），C（﹣2，0），点P是线段AB上方抛物线上的一个动点．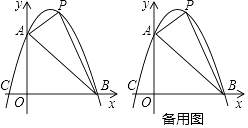

(1)、求抛物线的解析式；

(2)、当点P运动到什么位置时，△PAB的面积有最大值？

(3)、过点P作x轴的垂线，交线段AB于点D，再过点P做PE∥x轴交抛物线于点E，连结DE，请问是否存在点P使△PDE为等腰直角三角形？若存在，求出点P的坐标；若不存在，说明理由．

查看试题解析