贵州省遵义市2018年中考数学试卷

试卷更新日期：2018-08-07 类型：中考真卷

进入出卷网下载

一、选择题

1. 如果电梯上升5层记为+5．那么电梯下降2层应记为（）

A、+2 B、﹣2 C、+5 D、﹣5

查看试题解析
2. 观察下列几何图形，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2018年第二季度，遵义市全市生产总值约为532亿元，将数532亿用科学记数法表示为（）

A、 532×10⁸ B、5.32×10² C、5.32×10⁶ D、5.32×10¹⁰

查看试题解析
4. 下列运算正确的是（）

A、（﹣a²）³=﹣a⁵ B、a³•a⁵=a¹⁵ C、（﹣a²b³）²=a⁴b⁶ D、3a²﹣2a²=1

查看试题解析
5. 已知a∥b，某学生将一直角三角板放置如图所示，如果∠1=35°，那么∠2的度数为（）

A、35° B、55° C、56° D、65°

查看试题解析
6. 贵州省第十届运动会将于2018年8月8日在遵义市奥体中心开幕，某校有2名射击队员在比赛中的平均成绩均为9环，如果教练要从中选1名成绩稳定的队员参加比赛，那么还应考虑这2名队员选拔成绩的（）

A、方差 B、中位数 C、众数 D、最高环数

查看试题解析
7. 如图，直线y=kx+3经过点（2，0），则关于x的不等式kx+3＞0的解集是（）

A、x＞2 B、x＜2 C、x≥2 D、x≤2

查看试题解析
8. 若要用一个底面直径为10，高为12的实心圆柱体，制作一个底面和高分别与圆柱底面半径和高相同的圆锥，则该圆锥的侧面积为（）

A、60π B、65π C、78π D、120π

查看试题解析
9. 已知x₁ ， x₂是关于x的方程x²+bx﹣3=0的两根，且满足x₁+x₂﹣3x₁x₂=5，那么b的值为（）

A、4 B、﹣4 C、3 D、﹣3

查看试题解析
10. 如图，点P是矩形ABCD的对角线AC上一点，过点P作EF∥BC，分别交AB，CD于E，F，连接PB，PD．若AE=2，PF=8．则图中阴影部分的面积为（）

A、10 B、12 C、16 D、18

查看试题解析
11. 如图，直角三角形的直角顶点在坐标原点，∠OAB=30°，若点A在反比例函数y= $\frac{6}{x}$ （x＞0）的图象上，则经过点B的反比例函数解析式为（）

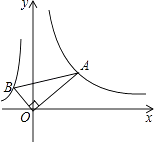A、y=﹣ $\frac{6}{x}$ B、y=﹣ $\frac{4}{x}$ C、y=﹣ $\frac{2}{x}$ D、y= $\frac{2}{x}$

查看试题解析
12. 如图，四边形ABCD中，AD∥BC，∠ABC=90°，AB=5，BC=10，连接AC，BD，以BD为直径的圆交AC于点E．若DE=3，则AD的长为（）

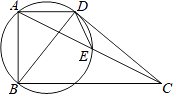A、5 B、4 C、3 $\sqrt{5}$ D、2 $\sqrt{5}$

查看试题解析

二、填空题

13. 计算 $\sqrt{9}$ ﹣1的结果是．

查看试题解析
14. 如图，△ABC中．点D在BC边上，BD=AD=AC，E为CD的中点．若∠CAE=16°，则∠B为度．

查看试题解析
15. 现有古代数学问题：“今有牛五羊二值金八两；牛二羊五值金六两，则一牛一羊值金两．

查看试题解析
16. 每一层三角形的个数与层数的关系如图所示，则第2018层的三角形个数为．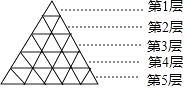

查看试题解析
17. 如图抛物线y=x²+2x﹣3与x轴交于A，B两点，与y轴交于点C，点P是抛物线对称轴上任意一点，若点D、E、F分别是BC、BP、PC的中点，连接DE，DF，则DE+DF的最小值为．

查看试题解析
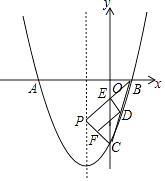18. 如图，在菱形ABCD中，∠ABC=120°，将菱形折叠，使点A恰好落在对角线BD上的点G处（不与B、D重合），折痕为EF，若DG=2，BG=6，则BE的长为．

查看试题解析

三、解答题

19. 2^﹣1+|1﹣ $\sqrt{8}$ |+（ $\sqrt{3}$ ﹣2）⁰﹣cos60°

查看试题解析
20. 化简分式（ $\frac{a^{2} - 3 a}{a^{2} - 6 a + 9}$ + $\frac{2}{3 - a}$ ）÷ $\frac{a - 2}{a^{2} - 9}$ ，并在2，3，4，5这四个数中取一个合适的数作为a的值代入求值．

查看试题解析
21. 如图，吊车在水平地面上吊起货物时，吊绳BC与地面保持垂直，吊臂AB与水平线的夹角为64°，吊臂底部A距地面1.5m．（计算结果精确到0.1m，参考数据sin64°≈0.90，cos64°≈0.44，tan64°≈2.05）

(1)、当吊臂底部A与货物的水平距离AC为5m时，吊臂AB的长为m．

(2)、如果该吊车吊臂的最大长度AD为20m，那么从地面上吊起货物的最大高度是多少？（吊钩的长度与货物的高度忽略不计）

查看试题解析
22. 为深化课程改革，某校为学生开设了形式多样的社团课程，为了解部分社团课程在学生中最受欢迎的程度，学校随机抽取七年级部分学生进行调查，从A：文学签赏，B：科学探究，C：文史天地，D：趣味数学四门课程中选出你喜欢的课程（被调查者限选一项），并将调查结果绘制成两个不完整的统计图，如图所示，根据以上信息，解答下列问题：

(1)、本次调查的总人数为人，扇形统计图中A部分的圆心角是度．

(2)、请补全条形统计图．

(3)、根据本次调查，该校七年级840名学生中，估计最喜欢“科学探究”的学生人数为多少？

查看试题解析
23. 某超市在端午节期间开展优惠活动，凡购物者可以通过转动转盘的方式享受折扣优惠，本次活动共有两种方式，方式一：转动转盘甲，指针指向A区域时，所购买物品享受9折优惠、指针指向其它区域无优惠；方式二：同时转动转盘甲和转盘乙，若两个转盘的指针指向每个区域的字母相同，所购买物品享受8折优惠，其它情况无优惠．在每个转盘中，指针指向每个区城的可能性相同（若指针指向分界线，则重新转动转盘）

(1)、若顾客选择方式一，则享受9折优惠的概率为；

(2)、若顾客选择方式二，请用树状图或列表法列出所有可能，并求顾客享受8折优惠的概率．

查看试题解析
24. 如图，正方形ABCD的对角线交于点O，点E、F分别在AB、BC上（AE＜BE），且∠EOF=90°，OE、DA的延长线交于点M，OF、AB的延长线交于点N，连接MN．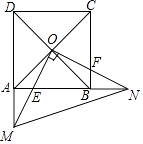

(1)、求证：OM=ON．

(2)、若正方形ABCD的边长为4，E为OM的中点，求MN的长．

查看试题解析
25. 在水果销售旺季，某水果店购进一优质水果，进价为20元/千克，售价不低于20元/千克，且不超过32元/千克，根据销售情况，发现该水果一天的销售量y（千克）与该天的售价x（元/千克）满足如下表所示的一次函数关系．
销售量y（千克）
…
34.8
32
29.6
28
…
售价x（元/千克）
…
22.6
24
25.2
26
…

(1)、某天这种水果的售价为23.5元/千克，求当天该水果的销售量．

(2)、如果某天销售这种水果获利150元，那么该天水果的售价为多少元？

查看试题解析
26. 如图，AB是半圆O的直径，C是AB延长线上的点，AC的垂直平分线交半圆于点D，交AC于点E，连接DA，DC．已知半圆O的半径为3，BC=2．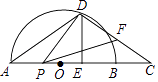

(1)、求AD的长．

(2)、点P是线段AC上一动点，连接DP，作∠DPF=∠DAC，PF交线段CD于点F．当△DPF为等腰三角形时，求AP的长．

查看试题解析
27. 在平面直角坐标系中，二次函数y=ax²+ $\frac{5}{3}$ x+c的图象经过点C（0，2）和点D（4，﹣2）．点E是直线y=﹣ $\frac{1}{3}$ x+2与二次函数图象在第一象限内的交点．

(1)、求二次函数的解析式及点E的坐标．

(2)、如图①，若点M是二次函数图象上的点，且在直线CE的上方，连接MC，OE，ME．求四边形COEM面积的最大值及此时点M的坐标．

(3)、如图②，经过A、B、C三点的圆交y轴于点F，求点F的坐标．

查看试题解析

销售量y（千克）	…	34.8	32	29.6	28	…
售价x（元/千克）	…	22.6	24	25.2	26	…