四川省峨眉山市2018届九年级数学中考二调考试试卷
试卷更新日期:2018-08-03 类型:中考模拟
一、单选题
-
1. 的相反数数是( )A、 B、 C、 D、2.
如图所示的几何体的俯视图是( )
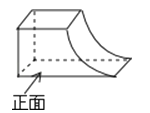 A、
A、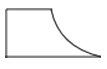 B、
B、 C、
C、 D、
D、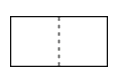 3. 下列计算正确的是( )A、 B、 C、 D、4. 如图, ∥ ,直线 分别交 、 于点 , , 平分 ,已知 ,则 =( )
3. 下列计算正确的是( )A、 B、 C、 D、4. 如图, ∥ ,直线 分别交 、 于点 , , 平分 ,已知 ,则 =( )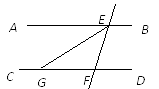 A、 B、 C、 D、5. 把 多项式分解因式,结果正确的是( )A、 B、 C、 D、6. 如图,已知 ,添加下列条件还不能判定 ≌ 的是( )
A、 B、 C、 D、5. 把 多项式分解因式,结果正确的是( )A、 B、 C、 D、6. 如图,已知 ,添加下列条件还不能判定 ≌ 的是( )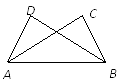 A、 B、 C、 D、7. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出 钱,会多 钱;每人出 钱,又会差 钱,问人数、物价各是多少?设合伙人数为 人,物价为 钱,以下列出的方程组正确的是( )A、 B、 C、 D、8. 如图,一次函数 ( 、 为常数,且 )与正比例函数 ( 为常数,且 )相交于点 ,则不等式 的解集是( )
A、 B、 C、 D、7. 《九章算术》是中国传统数学的重要著作,方程术是它的最高成就.其中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出 钱,会多 钱;每人出 钱,又会差 钱,问人数、物价各是多少?设合伙人数为 人,物价为 钱,以下列出的方程组正确的是( )A、 B、 C、 D、8. 如图,一次函数 ( 、 为常数,且 )与正比例函数 ( 为常数,且 )相交于点 ,则不等式 的解集是( ) A、 B、 C、 D、9. 在四边形 中, , , , 垂直平分 ,点 为垂足。设 , ,则 关于x的函数关系用图象大致可以表示为( )
A、 B、 C、 D、9. 在四边形 中, , , , 垂直平分 ,点 为垂足。设 , ,则 关于x的函数关系用图象大致可以表示为( ) A、
A、 B、
B、 C、
C、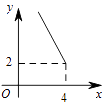 D、
D、 10. 如图, 与 均为正三角形,且顶点 , 均在双曲线 上,点 , 在 轴上,连结 交 于点 ,则 的面积是( )
10. 如图, 与 均为正三角形,且顶点 , 均在双曲线 上,点 , 在 轴上,连结 交 于点 ,则 的面积是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: =12. 当 时,二次根式 的值为 .13. 如图, 中, 等于 , , , 、 分别是 、 的中点,连结 ,则 的面积是
 14. 点 的坐标是 ,从 、 、 、 、 这五个数中任取一个数作为 的值,再从余下的四个数中任取一个数作为 的值,则点 在平面直角坐标系中第三象限的概率是15. 已知关于 的二次函数 的图象与 轴的一个交点坐标为 .若 ,则 的取值范围是
14. 点 的坐标是 ,从 、 、 、 、 这五个数中任取一个数作为 的值,再从余下的四个数中任取一个数作为 的值,则点 在平面直角坐标系中第三象限的概率是15. 已知关于 的二次函数 的图象与 轴的一个交点坐标为 .若 ,则 的取值范围是
16. 如果关于 的一元二次方程 有两个实数根,且其中一个根为另一个根的 倍,则称这样的方程为“倍根方程”.以下关于倍根方程的说法,正确的是(写出所有正确说法的序号)①方程 是倍根方程;②若方程 是倍根方程,则 ;③若点 在反比例函数 的图象上,则关于 的方程 是倍根方程;④若方程 是倍根方程,且相异两点 , 都在抛物线 上,则方程 的一个根是 .
三、解答题
-
17. 计算: .18. 解不等式组: .19. 如图,在□ 中, 、 分别为边 、 的中点, 是对角线,
求证: = .
 20. 化简 ,并求值,其中 与 、 构成 的三边,且 为整数.21. 李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
20. 化简 ,并求值,其中 与 、 构成 的三边,且 为整数.21. 李老师为了解学生完成数学课前预习的具体情况,对部分学生进行了跟踪调查,并将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.制成以下两幅不完整的统计图,请你根据统计图解答下列问题: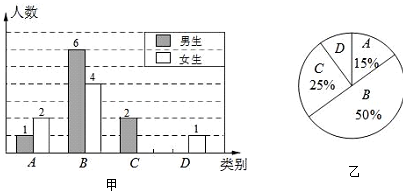 (1)、李老师一共调查了名同学?(2)、C类女生有名,D类男生有名,将下面条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
(1)、李老师一共调查了名同学?(2)、C类女生有名,D类男生有名,将下面条形统计图补充完整;(3)、为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
22. 如图,在一笔直的海岸线 上有 、 两个观测站, 在 的正东方向, (单位: )有一艘小船在点 处,从 测得小船在北偏西 的方向,从 测得小船在北偏东 的方向.(结果保留根号)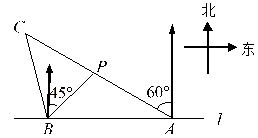 (1)、求点 到海岸线 的距离;(2)、小船从点 处沿射线 的方向航行一段时间后,到达点 处,此时,从 测得小船在北偏西 的方向,求点 与点 之间的距离.23. 如图,已知⊙ 的半径长为 , 、 是⊙ 的两条弦,且 = , 的延长线交 于点 ,联结 、 .
(1)、求点 到海岸线 的距离;(2)、小船从点 处沿射线 的方向航行一段时间后,到达点 处,此时,从 测得小船在北偏西 的方向,求点 与点 之间的距离.23. 如图,已知⊙ 的半径长为 , 、 是⊙ 的两条弦,且 = , 的延长线交 于点 ,联结 、 .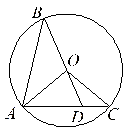 (1)、求证: ∽ ;(2)、记 、 、 的面积分别为 、 、 ,若 ,求 的长.
(1)、求证: ∽ ;(2)、记 、 、 的面积分别为 、 、 ,若 ,求 的长.
24. 如图(13),矩形 中, 、 、 ,射线 过点 且与 轴平行,点 、 分别是 和 轴正半轴上动点,满足 . (1)、①点 的坐标是;② =度;③当点 与点 重合时,点 的坐标为;
(1)、①点 的坐标是;② =度;③当点 与点 重合时,点 的坐标为;
(2)、设 的中点为 , 与线段 相交于点 ,连结 ,如图(13)乙所示,若 为等腰三角形,求点 的横坐标;
(3)、设点 的横坐标为 ,且 , 与矩形 的重叠部分的面积为 ,试求 与 的函数关系式.