四川省成都市青羊区2018届九年级数学中考二诊试卷
试卷更新日期：2018-08-03 类型：中考模拟
一、单选题
-
1. ﹣8的绝对值是（ ）A、﹣8 B、8 C、﹣ D、2. 成都第三绕城高速公路，主线起于蒲江境内的城雅高速公路，途经成都市14个区县，闭合于起点，串联起整个成都经济区．项目全长459公里，设计速度120公里/小时，总投资119000000元，用科学记数法表示总投资为（ ）A、119×106 B、1.19×107 C、1.19×108 D、1.19×1093. 某班派9名同学参加红五月歌咏比赛，他们的身高分别是（单位：厘米）：167，159，161，159，163，157，170，159，165．这组数据的众数和中位数分别是（ ）A、159，163 B、157，161 C、159，159 D、159，1614. 如图，在▱ABCD中，对角线AC，BD相交于点O，添加下列条件不能判定▱ABCD是菱形的只有（ ）
A、AC⊥BD B、AB=BC C、AC=BD D、∠1=∠25. 将抛物线y＝－2x2＋1向右平移1个单位长度，再向上平移1个单位长度所得的抛物线解析式为（ ）A、y＝－2(x＋1)2 B、y＝－2(x＋1)2＋2 C、y＝－2(x－1)2＋2 D、y＝－2(x－1)2＋16. 如图，将矩形纸片ABCD沿BD折叠，得到△BC′D，C′D与AB交于点E．若∠1=35°，则∠2的度数为（ ）
A、 B、 C、 D、7. 如图，已知直线a//b//c，分别交直线m、n于点A，C，E，B，D，F，AC＝4，CE＝6，BD＝3，则BF的长为（ ）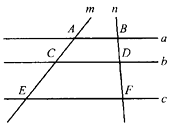
A、 B、 C、6 D、8. 已知：如图，在⊙O中，OA⊥BC，∠AOB=70°，则∠ADC的度数为（ ）
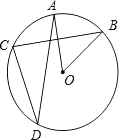A、30° B、35° C、45° D、70°二、填空题
-
9. 分解因式：mn2-2mn+m=10. 如图，在△ABC中，AB＝AC，BD平分∠ABC，交AC于点D。若BD＝BC，则∠A＝度.
11. 在平面直角坐标系xOy中，点A、B的坐标分别为（2，﹣1）、（3，0），以原点O为位似中心，把线段AB放大，点B的对应点B′的坐标为（6，0），则点A的对应点A′的坐标为
12. 如图，PA与⊙O相切，切点为A，PO交⊙O于点C，点B是优弧CBA上一点，若∠ABC=32°，则∠P的度数为 ．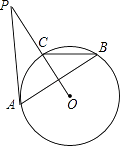
13. 若 +b2+2b+1=0，则a2+ ﹣|b|= ．14. 今年5月份有关部门对计划去上海迪士尼乐园的部分市民的前往方式进行调查，图1和图2是收集数据后绘制的两幅不完整统计图．根据图中提供的信息，那么本次调查的对象中选择公交前往的人数是
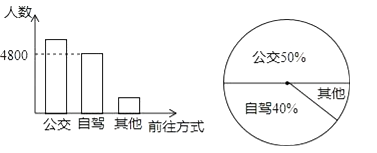15. 如图所示，⊙O是以坐标原点O为圆心，4为半径的圆，点P的坐标为（ ， ），弦AB经过点P，则图中阴影部分面积的最小值= ．
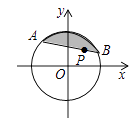16. 如图，已知四边形ABCD的一组对边AD、BC的延长线相交于点E．另一组对边AB、DC的延长线相交于点F，若cos∠ABC=cos∠ADC= ，CD=5，CF=ED=n，则AD的长为（用含n的式子表示）．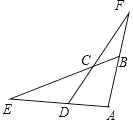
三、解答题
-
17.(1)、计算|﹣ |+ ×（ ）﹣1﹣2cos45°﹣（π﹣1）0(2)、解分式方程： ﹣3=18. 先化简，再求代数式 的值，其中19. 某校举办“汉字听写”大赛，现要从A、B两位男生和C、D两位女生中，选派学生代表本班参加大赛．(1)、如果随机选派一位学生参赛，那么四人中选派到男生B的概率是；(2)、如果随机选派两位学生参赛，求四人中恰好选派一男一女两位同学参赛的概率．20. 如图，在教学楼距地面8米高的窗口中C处，测得正前方旗杆顶部A点的仰角为37°，旗杆底部B点的俯角为45°.升旗时，国旗上端悬挂在距地面2米处.若国旗随国歌声冉冉升起，并在国歌播放40秒结束时到达旗杆顶端，则国旗应以多少米/秒的速度匀速上升？
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
21. 如图，一次函数y=kx+b的图象分别与反比例函数 的图象在第一象限交于点A（8，6），与y轴的负半轴交于点B，且OA＝OB.
(1)、求函数y=kx+b和 的表达式；(2)、已知点C（0，10），试在该一次函数图象上确定一点M，使得MB＝MC。求此时点M的坐标.22. 如图，点A、B、C、D是直径为AB的⊙O上的四个点，CD＝BC，AC与BD交于点E。
(1)、求证：DC2＝CE·AC；
(2)、若AE＝2EC，求 之值；
(3)、在（2）的条件下，过点C作⊙O的切线，交AB的延长线于点H，若S△ACH＝ ，求EC之长.23. 某商店经销一种空气净化器，每台净化器的成本价为200元．经过一段时间的销售发现，每月的销售量y（台）与销售单价x（元）的关系为y=﹣2x+800．(1)、该商店每月的利润为W元，写出利润W与销售单价x的函数关系式；
(2)、若要使每月的利润为20000元，销售单价应定为多少元？
(3)、商店要求销售单价不低于280元，也不高于350元，求该商店每月的最高利润和最低利润分别为多少？24. 在矩形ABCD中，AB＝8，AD＝12，M是AD边的中点，P是AB边上的一个动点（不与A、B重合），PM的延长线交射线CD于Q点，MN⊥PQ交射线BC于N点。
(1)、若点N在BC之间时，如图：
①求证：∠NPQ＝∠PQN；②请问 是否为定值？若是定值，求出该定值；若不是，请举反例说明；
(2)、当△PBN与△NCQ的面积相等时，求AP的值.25. 已知点A（－2，2），B（8，12）在抛物线y=ax2+bx上.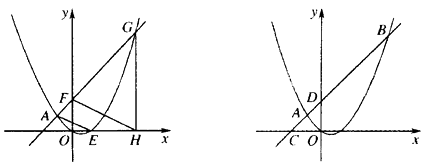
(1)、求抛物线的解析式；(2)、如图1，点F的坐标为（0，m）（m>4），直线AF交抛物线于另一点G，过点G作x轴的垂线，垂足为H，设抛物线与x轴的正半轴交于点E，连接FH、AE，求 之值（用含m的代数式表示）；(3)、如图2，直线AB分别交x轴、y轴于C、D两点，点P从点C出发，沿射线CD方向匀速运动，速度为每秒 个单位长度，同时点Q从原点O出发，沿x轴正方向匀速运动，速度为每秒1个单位长度，点M是直线PQ与抛物线的一个交点，当运动到t秒时，QM＝3PM，求t的值.