山东省滨州市2018届九年级数学中考模拟试卷

试卷更新日期：2018-08-03 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、a+a²=a³ B、（a³）²=a⁵ C、a•a²=a³ D、a⁶÷a²=a³

查看试题解析
2. 据悉，超级磁力风力发电机可以大幅度提升风力发电效率，但其造价高昂，每座磁力风力发电机，其建造花费估计要5 300万美元，“5 300万”用科学记数法可表示为（）

A、5.3×10³ B、5.3×10⁴ C、5.3×10⁷ D、5.3×10⁸

查看试题解析
3. $\sqrt[3]{64}$ 的平方根为（）

A、±8 B、±4 C、±2 D、4

查看试题解析
4. 用公式法解方程4y²=12y+3，得到（）

A、y= $\frac{- 3 \pm \sqrt{6}}{2}$ B、y= $\frac{3 \pm \sqrt{6}}{2}$ C、y= $\frac{- 3 \pm 2 \sqrt{3}}{2}$ D、y= $\frac{3 \pm 2 \sqrt{3}}{2}$

查看试题解析
5. 已知a、b、c是△ABC的三边长，且方程a（1+x²）+2bx﹣c（1﹣x²）=0的两根相等，则△ABC为（）

A、等腰三角形 B、直角三角形 C、等边三角形 D、任意三角形

查看试题解析
6. 某工厂接到加工600件衣服的订单，预计每天做25件，正好按时完成，后因客户要求提前3天交货，工人则需要提高每天的工作效率，设工人每天应多做x件，依题意列方程正确的是（）

A、 $\frac{600}{25 + x} - \frac{600}{25} = 3$ B、 $\frac{600}{25} + 3 = \frac{600}{x}$ C、 $\frac{600}{25} - \frac{600}{x} = 3$ D、 $\frac{600}{25} - \frac{600}{25 + x} = 3$

查看试题解析
7. 如图，港口A在观测站O的正东方向，某船从港口A出发，沿北偏东15°方向航行15 km到达B处，此时从观测站O处测得该船位于北偏东45°的方向，则观测站O距港口A的距离为（）

A、 $\frac{15 \sqrt{2}}{2}$ km B、15 $\sqrt{2}$ km C、 $\frac{15}{2}$ km D、15 km

查看试题解析
8. 如图是根据某班50名同学一周的体育锻炼情况绘制的条形统计图，则这个班50名同学一周参加体育锻炼时间的众数与中位数分别为（）

A、9，8 B、8，9 C、8，8.5 D、19，17

查看试题解析
9. 如图，在△ABC中，中线BE，CD相交于点O，连线DE，下列结论：
① $\frac{D E}{B C} = \frac{1}{2}$ ； ② $\frac{S_{△ A D E}}{S_{△ A B C}} = \frac{1}{2}$ ； ③ $\frac{A D}{A B} = \frac{O E}{O D}$ ； ④ $\frac{S_{△ O D E}}{S_{△ D E C}} = \frac{1}{4}$ 其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 抛物线y=ax²+bx+c交x轴于A（﹣1，0），B（3，0），交y轴的负半轴于C，顶点为D．下列结论：①2a+b=0；②2c＜3b；③当m≠1时，a+b＜am²+bm；④当△ABD是等腰直角三角形时，则a= $\frac{1}{2}$ ；⑤当△ABC是等腰三角形时，a的值有3个．其中正确的有（）个.

A、2 B、3 C、4 D、5

查看试题解析
11. 已知“！”是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1=24，…若公式 C_n^m= $\frac{n!}{m! (n - m)!}$ （n＞m），则C₁₂⁵+C₁₂⁶=（）

A、 $C_{13}^{5}$ B、 $C_{13}^{6}$ C、 $C_{13}^{11}$ D、 $C_{12}^{7}$

查看试题解析

二、填空题

12. 计算：（ $\frac{1}{2}$ ）^﹣2﹣|1﹣ $\sqrt{3}$ |﹣（π﹣2015）⁰﹣2sin60°+ $\sqrt{12}$ = ．

查看试题解析
13. 若3x^3m+5n+9+9y^4m^﹣2n+3=5是二元一次方程，则 $\frac{m}{n}$ = ．

查看试题解析
14. 已知3，a，4，b，5这五个数据，其中a，b是方程x²﹣3x+2=0的两个根，则这五个数据的方差是．

查看试题解析
15. 在同一平面内，∠AOB=120°，射线OC与∠AOB的一边所成夹角为直角，射线OM平分∠BOC，则∠AOM的度数为．

查看试题解析
16. 如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点E处，连接DE交AB于点F，当△DEB是直角三角形时，DF的长为．

查看试题解析
17. [x）表示大于x的最小整数，如[2.3）=3，[﹣4）=﹣3，则下列判断：①[﹣8 $\frac{3}{5}$ ）=﹣9；②[x）﹣x有最大值是1；③[x）﹣x有最小值是0；④x＜[x）≤x+1，其中正确的是（填编号）．

查看试题解析
18. 观察，分析，猜想并对猜想的正确性予以说明．
1×2×3×4+1=5²
2×3×4×5+1=11²
3×4×5×6+1=19²
4×5×6×7+1=29²
n（n+1）（n+2）（n+3）+1=（n为整数）

查看试题解析
19. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以点A为圆心，AC的长为半径作 $\vec{C E}$ 交AB于点E，以点B为圆心，BC的长为半径作 $\vec{C D}$ 交AB于点D，则阴影部分的面积为．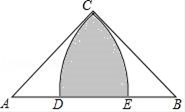

查看试题解析

三、解答题

20.

(1)、化简：（ $\frac{3}{a + 1}$ ﹣a+1）÷ $\frac{a^{2} - 4 a + 4}{a + 1}$ .

(2)、解不等式组： ${\begin{matrix} x - 1 > 4 x + 2 \\ \frac{2 x + 1}{3} > 2 x \end{matrix}$

查看试题解析
21. 某县教育局为了丰富初中学生的大课间活动，要求各学校开展形式多样的阳光体育活动．某中学就“学生体育活动兴趣爱好”的问题，随机调查了本校某班的学生，并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图：

(1)、在这次调查中，喜欢篮球项目的同学有多少人？

(2)、在扇形统计图中，“乒乓球”的百分比为多少？

(3)、如果学校有800名学生，估计全校学生中有多少人喜欢篮球项目？

(4)、请将条形统计图补充完整．

(5)、在被调查的学生中，喜欢篮球的有2名女同学，其余为男同学．现要从中随机抽取2名同学代表班级参加校篮球队，请运用列表或树状图求出所抽取的2名同学恰好是1名女同学和1名男同学的概率．

查看试题解析
22. 已知：如图，在▱ABCD中，E，F分别是边AD，BC上的点，且AE=CF，直线EF分别交BA的延长线、DC的延长线于点G，H，交BD于点O．

(1)、求证：△ABE≌△CDF；

(2)、连接DG，若DG=BG，则四边形BEDF是什么特殊四边形？请说明理由．

查看试题解析
23. 已知：如图，斜坡AP的坡度为1：2.4，坡长AP为26米，在坡顶A处的同一水平面上有一座古塔BC，在斜坡底P处测得该塔的塔顶B的仰角为45°，在坡顶A处测得该塔的塔顶B的仰角为76°．求：

(1)、坡顶A到地面PQ的距离；

(2)、古塔BC的高度（结果精确到1米）．（参考数据：sin76°≈0.97，cos76°≈0.24，tan76°≈4.01）

查看试题解析
24. 已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．

(1)、求证：BD是⊙O的切线；

(2)、求证：CE²=EH•EA；

(3)、若⊙O的半径为 $\frac{5}{2}$ ，sinA= $\frac{3}{5}$ ，求BH的长．

查看试题解析
25. 如图，抛物线y=ax²+bx﹣3与x轴交于A，B两点，与y轴交于C点，且经过点（2，﹣3a），对称轴是直线x=1，顶点是M．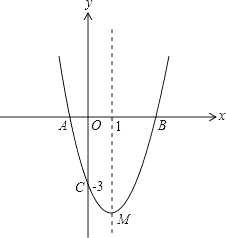

(1)、求抛物线对应的函数表达式；

(2)、经过C，M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，使以点P，A，C，N为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、设直线y=﹣x+3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；

(4)、当E是直线y=﹣x+3上任意一点时，（3）中的结论是否成立（请直接写出结论）．

查看试题解析