内蒙古鄂尔多斯市2018届九年级数学中考模拟试卷(一)
试卷更新日期:2018-08-03 类型:中考模拟
一、单选题
-
1. 已知数a、b、c在数轴上的位置如图所示,化简|a+b|﹣|c﹣b|的结果是( )
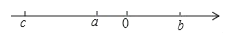 A、a+b B、﹣a﹣c C、a+c D、a+2b﹣c2. 某种细胞的平均直径是0.00000085米,将0.00000085用科学记数法表示为( )A、8.5×10﹣7 B、0.85×10﹣7 C、8.5×10﹣6 D、85×10﹣63. 下列计算正确的是( )
A、a+b B、﹣a﹣c C、a+c D、a+2b﹣c2. 某种细胞的平均直径是0.00000085米,将0.00000085用科学记数法表示为( )A、8.5×10﹣7 B、0.85×10﹣7 C、8.5×10﹣6 D、85×10﹣63. 下列计算正确的是( )
A、22018(﹣0.5)2017=﹣2 B、a3+a3=a6 C、a5a2=a10 D、4. 从一副扑克牌中随机抽出一张牌,得到梅花或者K的概率是( )
A、 B、 C、 D、5. 如图,M在BC上,MB= MC,如果△ABC绕点M按顺时针方向旋转180°后与△FED重合,则以下结论中不正确的是( )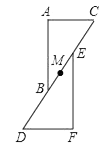 A、△ABC和△FED的面积相等 B、△ABC和△FED的周长相等 C、∠A+∠ABC=∠F+∠FDE D、AC∥DF,且AC=DF6. 在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的最少个数为 ,最多个数为 ,下列正确的是( )
A、△ABC和△FED的面积相等 B、△ABC和△FED的周长相等 C、∠A+∠ABC=∠F+∠FDE D、AC∥DF,且AC=DF6. 在桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,设组成这个几何体的小正方体的最少个数为 ,最多个数为 ,下列正确的是( )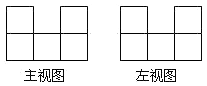 A、 , B、 , C、 , D、 ,7. 如图.在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于MN一半的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )
A、 , B、 , C、 , D、 ,7. 如图.在△ABC中,∠C=90°,按以下步骤作图:①以点A为圆心、适当长为半径作圆弧,分别交边AC,AB于点M、N;②分别以点M和点N为圆心、大于MN一半的长为半径作圆弧,在∠BAC内,两弧交于点P;③作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( )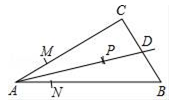 A、15 B、30 C、45 D、608. 小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A、15 B、30 C、45 D、608. 小明坐滴滴打车前去火车高铁站,小明可以选择两条不同路线:路线A的全程是25千米,但交通比较拥堵,路线B的全程比路线A的全程多7千米,但平均车速比走路线A时能提高60%,若走路线B的全程能比走路线A少用15分钟.若设走路线A时的平均速度为x千米/小时,根据题意,可列分式方程( )
A、 =15 B、 =15 C、 = D、 =9. 如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧AMB上一点,则sin∠APB的值为( )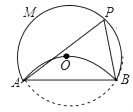 A、 B、 C、 D、110. 如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )
A、 B、 C、 D、110. 如图,等边△ABC的边长为2cm,点P从点A出发,以1cm/s的速度沿AC向点C运动,到达点C停止;同时点Q从点A出发,以2cm/s的速度沿AB﹣BC向点C运动,到达点C停止,设△APQ的面积为y(cm2),运动时间为x(s),则下列最能反映y与x之间函数关系的图象是( )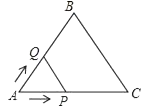 A、
A、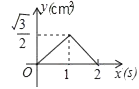 B、
B、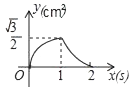 C、
C、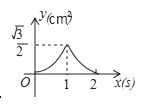 D、
D、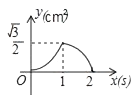
二、填空题
-
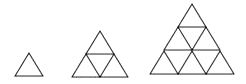
11. 已知函数 ,则x取值范围是 .12. 计算: = .13. 如图,用火柴摆上系列图案,按这种方式摆下去,当每边摆5根时,有个三角形.
 14. 已知a,b,c分别是三角形的三边,则方程(a+b)x2+2cx+(a+b)=0的根的情况是 .15. 如图,已知直线 与坐标轴交于A,B两点,矩形ABCD的对称中心为M,双曲线 (x>0)正好经过C,M两点,则直线AC的解析式为: .
14. 已知a,b,c分别是三角形的三边,则方程(a+b)x2+2cx+(a+b)=0的根的情况是 .15. 如图,已知直线 与坐标轴交于A,B两点,矩形ABCD的对称中心为M,双曲线 (x>0)正好经过C,M两点,则直线AC的解析式为: .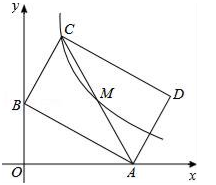 16. 如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN= . 证明:DN2+BM2=MN2 .
16. 如图,正方形ABCD中,∠EAF=45°,连接对角线BD交AE于M,交AF于N,若DN=1,BM=2,那么MN= . 证明:DN2+BM2=MN2 .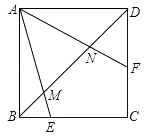
三、解答题
-
17. 先化简,再求值: ,其中m是方程x2+x﹣3=0的根.
18. 某校为进一步推进“一校一球队、一级一专项、一人一技能”的体育活动,决定对学生感兴趣的球类项目(A:足球,B:篮球,C:排球,D:羽毛球,E:乒乓球)进行问卷调查,学生可根据自己的喜好选修一门,李老师对某班全班同学的选课情况进行统计后,制成了两幅不完整的统计图(如图).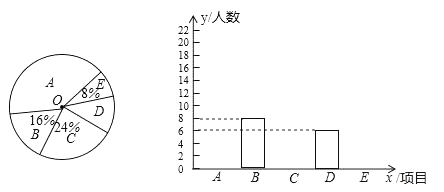 (1)、该班对足球和排球感兴趣的人数分别是、;(2)、若该校共有学生3500名,请估计有多少人选修足球?(3)、该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.19. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题:
(1)、该班对足球和排球感兴趣的人数分别是、;(2)、若该校共有学生3500名,请估计有多少人选修足球?(3)、该班班委5人中,1人选修篮球,3人选修足球,1人选修排球,李老师要从这5人中任选2人了解他们对体育选修课的看法,请你用列表或画树状图的方法,求选出的2人恰好1人选修篮球,1人选修足球的概率.19. 某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光明且温度为18℃的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线 的一部分.请根据图中信息解答下列问题: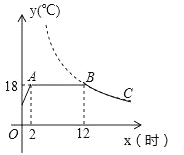 (1)、恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(1)、恒温系统在这天保持大棚内温度18℃的时间有多少小时?
(2)、求k的值;(3)、当x=15时,大棚内的温度约为多少度?20. 工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)、该工艺品每件的进价、标价分别是多少元?(2)、若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?21. 某校计划把一块近似于直角三角形的废地开发为生物园,如图所示,∠ACB=90°,BC=60米,∠A=36°.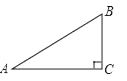 (1)、若入口处E在AB边上,且与A、B等距离,求CE的长(精确到个位);
(1)、若入口处E在AB边上,且与A、B等距离,求CE的长(精确到个位);
(2)、若D点在AB边上,计划沿线段CD修一条水渠.已知水渠的造价为50元/米,水渠路线应如何设计才能使造价最低,求出最低造价.(其中sin36°=0.5878,cos36°=0.8090,tan36°=0.7265)
22. 如图,⊙O的半径为6cm,经过⊙O上一点C作⊙O的切线交半径OA的延长于点B,作∠ACO的平分线交⊙O于点D,交OA于点F,延长DA交BC于点E.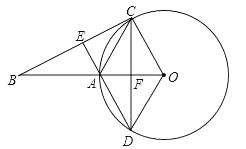 (1)、求证:AC∥OD;(2)、如果DE⊥BC,求弧AC的长度.23. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b.
(1)、求证:AC∥OD;(2)、如果DE⊥BC,求弧AC的长度.23. 已知,抛物线y=ax2+ax+b(a≠0)与直线y=2x+m有一个公共点M(1,0),且a<b. (1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(1)、求b与a的关系式和抛物线的顶点D坐标(用a的代数式表示);
(2)、直线与抛物线的另外一个交点记为N,求△DMN的面积与a的关系式;
(3)、a=﹣1时,直线y=﹣2x与抛物线在第二象限交于点G,点G、H关于原点对称,现将线段GH沿y轴向上平移t个单位(t>0),若线段GH与抛物线有两个不同的公共点,试求t的取值范围.24. 在△ABC中,AB=AC,点D是直线BC上的一点(不与B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠BCE=β.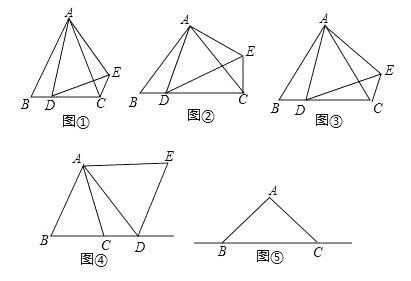 (1)、如图①,当点D在线段BC上,如果α=60°,β=120°;
(1)、如图①,当点D在线段BC上,如果α=60°,β=120°;如图②,当点D在线段BC上,如果α=90°,β=90°
如图③,当点D在线段BC上,如果α,β之间有什么样的关系?请直接写出.
(2)、如图④,当点D在射线BC上,(1)中结论是否成立?请说明理由.(3)、如图⑤,当点D在射线CB上,且在线段BC外,(1)中结论是否成立?若不成立,请直接写出你认为正确的结论.