山东省东营市2018年中考数学试卷

试卷更新日期：2018-08-03 类型：中考真卷

进入出卷网下载

一、选择题

1. 下列运算正确的是（）

A、﹣（x﹣y）²=﹣x²﹣2xy﹣y² B、a²+a²=a⁴ C、a²•a³=a⁶ D、（xy²）²=x²y⁴

查看试题解析
2. 在平面直角坐标系中，若点P（m﹣2，m+1）在第二象限，则m的取值范围是（）

A、m＜﹣1 B、m＞2 C、﹣1＜m＜2 D、m＞﹣1

查看试题解析
3. 为了帮助市内一名患“白血病”的中学生，东营市某学校数学社团15名同学积极捐款，捐款情况如下表所示，下列说法正确的是（）
捐款数额
10
20
30
50
100
人数
2
4
5
3
1

A、众数是100 B、中位数是30 C、极差是20 D、平均数是30

查看试题解析
4. 小岩打算购买气球装扮学校“毕业典礼”活动会场，气球的种类有笑脸和爱心两种，两种气球的价格不同，但同一种气球的价格相同．由于会场布置需要，购买时以一束（4个气球）为单位，已知第一、二束气球的价格如图所示，则第三束气球的价格为（）

A、19 B、18 C、16 D、15

查看试题解析
5.
如图，在四边形ABCD中，E是BC边的中点，连接DE并延长，交AB的延长线于F点，AB＝BF.添加一个条件，使四边形ABCD是平行四边形．你认为下面四个条件中可选择的是（）

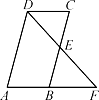A、AD＝BC B、CD＝BF C、∠A＝∠C D、∠F＝∠CDE

查看试题解析
6. 如图所示，圆柱的高AB=3，底面直径BC=3，现在有一只蚂蚁想要从A处沿圆柱表面爬到对角C处捕食，则它爬行的最短距离是（）

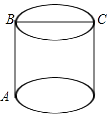A、 $3 \sqrt{1 + π}$ B、 $3 \sqrt{2}$ C、 $\frac{3 \sqrt{4 + π^{2}}}{2}$ D、 $3 \sqrt{1 + π^{2}}$

查看试题解析
7. 如图所示，已知△ABC中，BC=12，BC边上的高h=6，D为BC上一点，EF∥BC，交AB于点E，交AC于点F，设点E到边BC的距离为x．则△DEF的面积y关于x的函数图象大致为（）

A、 B、 C、 D、

查看试题解析
8. 如图，点E在△DBC的边DB上，点A在△DBC内部，∠DAE=∠BAC=90°，AD=AE，AB=AC．给出下列结论：
①BD=CE；②∠ABD+∠ECB=45°；③BD⊥CE；④BE²=2（AD²+AB²）﹣CD² ．其中正确的是（）

A、①②③④ B、②④ C、①②③ D、①③④

查看试题解析

二、填空题

9. 东营市大力推动新旧动能转换，产业转型升级迈出新步伐．建立了新旧动能转换项目库，筛选论证项目377个，计划总投资4147亿元.4147亿元用科学记数法表示为元．

查看试题解析
10. 分解因式：x³﹣4xy²= ．

查看试题解析
11. 有五张背面完全相同的卡片，其正面分别画有等腰三角形、平行四边形、矩形、正方形、菱形，将这五张卡片背面朝上洗匀，从中随机抽取一张，卡片上的图形是中心对称图形的概率是．

查看试题解析
12. 如图，B（3，﹣3），C（5，0），以OC，CB为边作平行四边形OABC，则经过点A的反比例函数的解析式为．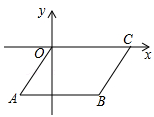

查看试题解析
13. 如图，在Rt△ABC中，∠B=90°，以顶点C为圆心，适当长为半径画弧，分别交AC，BC于点E，F，再分别以点E，F为圆心，大于 $\frac{1}{2}$ EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D．若BD=3，AC=10，则△ACD的面积是．

查看试题解析
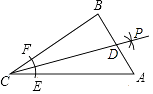14. 已知一个圆锥体的三视图如图所示，则这个圆锥体的侧面积为．

查看试题解析
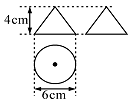15. 在平面直角坐标系内有两点A、B，其坐标为A（﹣1，﹣1），B（2，7），点M为x轴上的一个动点，若要使MB﹣MA的值最大，则点M的坐标为．

查看试题解析
16. 如图，在平面直角坐标系中，点A₁ ， A₂ ， A₃ ， …和B₁ ， B₂ ， B₃ ， …分别在直线y= $\frac{1}{5}$ x+b和x轴上．△OA₁B₁ ， △B₁A₂B₂ ， △B₂A₃B₃ ， …都是等腰直角三角形．如果点A₁（1，1），那么点A₂₀₁₈的纵坐标是．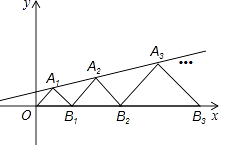

查看试题解析

三、解答题

17.

(1)、计算：|2﹣ $\sqrt{3}$ |+（ $\sqrt{2}$ +1）⁰﹣3tan30°+（﹣1）²⁰¹⁸﹣（ $\frac{1}{2}$ ）^﹣¹；

(2)、解不等式组： ${\begin{matrix} \end{matrix} \begin{matrix} x + 3 > 0 \\ 2 (x - 1) + 3 \geq 3 x \end{matrix}$ 并判断﹣1， $\sqrt{2}$ 这两个数是否为该不等式组的解．

查看试题解析
18. 2018年东营市教育局在全市中小学开展了“情系疏勒书香援疆”捐书活动，200多所学校的师生踊跃参与，向新疆疏勒县中小学共捐赠爱心图书28.5万余本．某学校学生社团对本校九年级学生所捐图书进行统计，根据收集的数据绘制了下面不完整的统计图表．请你根据统计图表中所提供的信息解答下列问题：
图书种类
频数（本）
频率
名人传记
175
a
科普图书
b
0.30
小说
110
c
其他
65
d

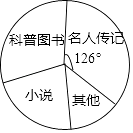(1)、求该校九年级共捐书多少本；

(2)、统计表中的a= ， b= ， c= ， d=；

(3)、若该校共捐书1500本，请估计“科普图书”和“小说”一共多少本；

(4)、该社团3名成员各捐书1本，分别是1本“名人传记”，1本“科普图书”，1本“小说”，要从这3人中任选2人为受赠者写一份自己所捐图书的简介，请用列表法或树状图求选出的2人恰好1人捐“名人传记”，1人捐“科普图书”的概率．

查看试题解析
19. 小明和小刚相约周末到雪莲大剧院看演出，他们的家分别距离剧院1200m和2000m，两人分别从家中同时出发，已知小明和小刚的速度比是3：4，结果小明比小刚提前4min到达剧院．求两人的速度．

查看试题解析
20. 如图，CD是⊙O的切线，点C在直径AB的延长线上．

(1)、求证：∠CAD=∠BDC；

(2)、若BD= $\frac{2}{3}$ AD，AC=3，求CD的长．

查看试题解析
21. 关于x的方程2x²﹣5xsinA+2=0有两个相等的实数根，其中∠A是锐角三角形ABC的一个内角．

(1)、求sinA的值；

(2)、若关于y的方程y²﹣10y+k²﹣4k+29=0的两个根恰好是△ABC的两边长，求△ABC的周长．

查看试题解析
22. 如图

(1)、某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO= $3 \sqrt{3}$ ，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB=°，AB= ．

(2)、请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO= $3 \sqrt{3}$ ，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．

查看试题解析
23. 如图，抛物线y=a（x﹣1）（x﹣3）（a＞0）与x轴交于A、B两点，抛物线上另有一点C在x轴下方，且使△OCA∽△OBC．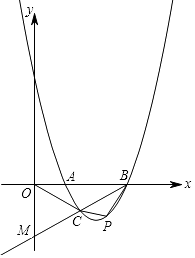

(1)、求线段OC的长度；

(2)、设直线BC与y轴交于点M，点C是BM的中点时，求直线BM和抛物线的解析式；

(3)、在（2）的条件下，直线BC下方抛物线上是否存在一点P，使得四边形ABPC面积最大？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析

图书种类	频数（本）	频率
名人传记	175	a
科普图书	b	0.30
小说	110	c
其他	65	d

捐款数额	10	20	30	50	100
人数	2	4	5	3	1