湖南省湘西州2018年中考数学试卷
试卷更新日期:2018-08-03 类型:中考真卷
一、填空题
-
1. ﹣2018的绝对值是 .2. 分解因式:a2﹣9= .3. 要使分式 有意义,则x的取值范围为 .
4. “可燃冰”作为新型能源,有着巨大的开发使用潜力,1千克“可燃冰”完全燃烧放出的热量约为420000000焦耳,数据420000000用科学记数法表示为 .5. 农历五月初五为端午节,端午节吃粽子是中华民族的传统习俗.小明妈妈买了3个红豆粽、2个碱水粽、5个腊肉粽,粽子除了内部馅料不同外其他均相同.小明随意吃了一个,则吃到腊肉棕的概率为 .
6. 按照如图的操作步骤,若输入x的值为2,则输出的值是 . (用科学计算器计算或笔算) 7. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .
7. 如图,DA⊥CE于点A,CD∥AB,∠1=30°,则∠D= .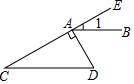 8. 对于任意实数a、b,定义一种运算:a※b=ab﹣a+b﹣2.例如,2※5=2×5﹣2+5﹣2=ll.请根据上述的定义解决问题:若不等式3※x<2,则不等式的正整数解是 .
8. 对于任意实数a、b,定义一种运算:a※b=ab﹣a+b﹣2.例如,2※5=2×5﹣2+5﹣2=ll.请根据上述的定义解决问题:若不等式3※x<2,则不等式的正整数解是 .
二、选择题
-
9. 下列运算中,正确的是( )A、a2•a3=a5 B、2a﹣a=2 C、(a+b)2=a2+b2 D、2a+3b=5ab10. 如图所示的几何体的主视图是( )
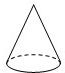 A、
A、 B、
B、 C、
C、 D、
D、 11. 在某次体育测试中,九年级(1)班5位同学的立定跳远成绩(单位:m)分别为:1.81,1.98,2.10,2.30,2.10.这组数据的众数为( )
11. 在某次体育测试中,九年级(1)班5位同学的立定跳远成绩(单位:m)分别为:1.81,1.98,2.10,2.30,2.10.这组数据的众数为( )
A、2.30 B、2.10 C、1.98 D、1.8112. 不等式组 的解集在数轴上表示正确的是( )
A、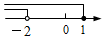 B、
B、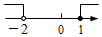 C、
C、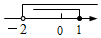 D、
D、 13. 一次函数y=x+2的图象与x轴的交点坐标为( )
13. 一次函数y=x+2的图象与x轴的交点坐标为( )
A、(0,2) B、(0,﹣2) C、(2,0) D、(﹣2,0)14. 下列四个图形中,是轴对称图形的是( )
A、 B、
B、 C、
C、 D、
D、 15. 已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
15. 已知⊙O的半径为5cm,圆心O到直线l的距离为5cm,则直线l与⊙O的位置关系为( )
A、相交 B、相切 C、相离 D、无法确定16. 若关于x的一元二次方程x2﹣2x+m=0有一个解为x=﹣1,则另一个解为( )
A、1 B、﹣3 C、3 D、417. 下列说法中,正确个数有( )①对顶角相等;②两直线平行,同旁内角相等;③对角线互相垂直的四边形为菱形;④对角线互相垂直平分且相等的四边形为正方形.
A、1个 B、2个 C、3个 D、4个18. 如图,直线AB与⊙O相切于点A,AC、CD是⊙O的两条弦,且CD∥AB,若⊙O的半径为5,CD=8,则弦AC的长为( )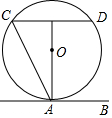 A、10 B、8 C、4 D、4
A、10 B、8 C、4 D、4三、解答题
-
19. 计算: +(π﹣2018)0﹣2tan45°20. 解方程组:21. 如图,在矩形ABCD中,E是AB的中点,连接DE、CE.
 (1)、求证:△ADE≌△BCE;(2)、若AB=6,AD=4,求△CDE的周长.22. 中华文化源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中抽取n名学生进行调查.根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
(1)、求证:△ADE≌△BCE;(2)、若AB=6,AD=4,求△CDE的周长.22. 中华文化源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中抽取n名学生进行调查.根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题: (1)、求n的值;(2)、请将条形统计图补充完整;
(1)、求n的值;(2)、请将条形统计图补充完整;
(3)、若该校共有2000名学生,请估计该校四大古典名著均已读完的人数.
23. 如图,某市郊外景区内一条笔直的公路l经过A、B两个景点,景区管委会又开发了风景优美的景点C.经测量,C位于A的北偏东60°的方向上,C位于B的北偏东30°的方向上,且AB=10km.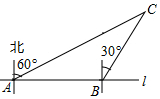 (1)、求景点B与C的距离;(2)、为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
(1)、求景点B与C的距离;(2)、为了方便游客到景点C游玩,景区管委会准备由景点C向公路l修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
24. 反比例函数y= (k为常数,且k≠0)的图象经过点A(1,3)、B(3,m).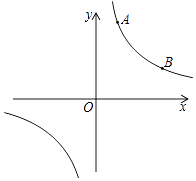 (1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.25. 某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、求反比例函数的解析式及B点的坐标;(2)、在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标.25. 某商店销售A型和B型两种电脑,其中A型电脑每台的利润为400元,B型电脑每台的利润为500元.该商店计划再一次性购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、求y关于x的函数关系式;(2)、该商店购进A型、B型电脑各多少台,才能使销售总利润最大,最大利润是多少?
(3)、实际进货时,厂家对A型电脑出厂价下调a(0<a<200)元,且限定商店最多购进A型电脑60台,若商店保持同种电脑的售价不变,请你根据以上信息,设计出使这100台电脑销售总利润最大的进货方案.
26. 如图1,经过原点O的抛物线y=ax2+bx(a、b为常数,a≠0)与x轴相交于另一点A(3,0).直线l:y=x在第一象限内和此抛物线相交于点B(5,t),与抛物线的对称轴相交于点C.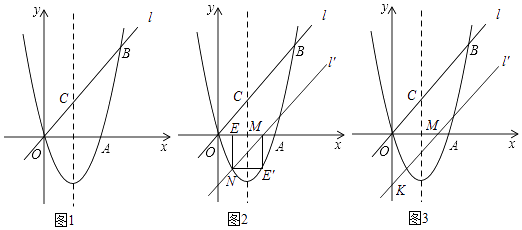 (1)、求抛物线的解析式;(2)、在x轴上找一点P,使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似,求满足条件的点P的坐标;(3)、直线l沿着x轴向右平移得到直线l′,l′与线段OA相交于点M,与x轴下方的抛物线相交于点N,过点N作NE⊥x轴于点E.把△MEN沿直线l′折叠,当点E恰好落在抛物线上时(图2),求直线l′的解析式;(4)、在(3)问的条件下(图3),直线l′与y轴相交于点K,把△MOK绕点O顺时针旋转90°得到△M′OK′,点F为直线l′上的动点.当△M'FK′为等腰三角形时,求满足条件的点F的坐标.
(1)、求抛物线的解析式;(2)、在x轴上找一点P,使以点P、O、C为顶点的三角形与以点A、O、B为顶点的三角形相似,求满足条件的点P的坐标;(3)、直线l沿着x轴向右平移得到直线l′,l′与线段OA相交于点M,与x轴下方的抛物线相交于点N,过点N作NE⊥x轴于点E.把△MEN沿直线l′折叠,当点E恰好落在抛物线上时(图2),求直线l′的解析式;(4)、在(3)问的条件下(图3),直线l′与y轴相交于点K,把△MOK绕点O顺时针旋转90°得到△M′OK′,点F为直线l′上的动点.当△M'FK′为等腰三角形时,求满足条件的点F的坐标.