湖南省邵阳市2018年中考数学试卷
试卷更新日期：2018-08-03 类型：中考真卷
一、选择题
-
1. 用计算器依次按键
，得到的结果最接近的是（ ）
A、1.5 B、1.6 C、1.7 D、1.82. 如图所示，直线AB，CD相交于点O，已知∠AOD=160°，则∠BOC的大小为（ ）
A、20° B、60° C、70° D、160°3. 将多项式x﹣x3因式分解正确的是（ ）
A、x（x2﹣1） B、x（1﹣x2） C、x（x+1）（x﹣1） D、x（1+x）（1﹣x）4. 下列图形中，是轴对称图形的是（ ）
A、
B、
C、
D、
5. 据《经济日报》2018年5月21日报道：目前，世界集成电路生产技术水平最高已达到7nm（1nm=10﹣9m），主流生产线的技术水平为14～28nm，中国大陆集成电路生产技术水平最高为28nm．将28nm用科学记数法可表示为（ ）
A、28×10﹣9m B、2.8×10﹣8m C、28×109m D、2.8×108m6. 如图所示，四边形ABCD为⊙O的内接四边形，∠BCD=120°，则∠BOD的大小是（ ）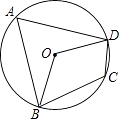
A、80° B、120° C、100° D、90°7. 小明参加100m短跑训练，2018年1～4月的训练成绩如下表所示：月份
1
2
3
4
成绩（s）
15.6
15.4
15.2
15
体育老师夸奖小明是“田径天才”，请你预测小明5年（60个月）后100m短跑的成绩为（ ）（温馨提示；目前100m短跑世界记录为9秒58）
A、14.8s B、3.8s C、3s D、预测结果不可靠8. 如图所示，在平面直角坐标系中，已知点A（2，4），过点A作AB⊥x轴于点B．将△AOB以坐标原点O为位似中心缩小为原图形的 ，得到△COD，则CD的长度是（ ）
A、2 B、1 C、4 D、29. 根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图．
根据图所提供的信息，若要推荐一位成绩较稳定的选手去参赛，应推荐（ ）
A、李飞或刘亮 B、李飞 C、刘亮 D、无法确定10. 程大位是我国明朝商人，珠算发明家．他60岁时完成的《直指算法统宗》是东方古代数学名著，详述了传统的珠算规则，确立了算盘用法．书中有如下问题：一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚得几丁．意思是：有100个和尚分100个馒头，如果大和尚1人分3个，小和尚3人分1个，正好分完，大、小和尚各有多少人，下列求解结果正确的是（ ）
A、大和尚25人，小和尚75人 B、大和尚75人，小和尚25人 C、大和尚50人，小和尚50人 D、大、小和尚各100人二、填空题
-
11. 点A在数轴上的位置如图所示，则点A表示的数的相反数是 ．
12. 如图所示，点E是平行四边形ABCD的边BC延长线上一点，连接AE，交CD于点F，连接BF．写出图中任意一对相似三角形： ．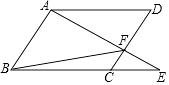
13. 已知关于x的方程x2+3x﹣m=0的一个解为﹣3，则它的另一个解是 ．
14. 如图所示，在四边形ABCD中，AD⊥AB，∠C=110°，它的一个外角∠ADE=60°，则∠B的大小是 ．
15. 某市对九年级学生进行“综合素质”评价，评价结果分为A，B，C，D，E五个等级．现随机抽取了500名学生的评价结果作为样本进行分析，绘制了如图所示的统计图．已知图中从左到右的五个长方形的高之比为2：3：3：1：1，据此估算该市80000名九年级学生中“综合素质”评价结果为“A”的学生约为人．
16. 如图所示，一次函数y=ax+b的图象与x轴相交于点（2，0），与y轴相交于点（0，4），结合图象可知，关于x的方程ax+b=0的解是 ．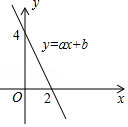
17. 如图所示，在等腰△ABC中，AB=AC，∠A=36°，将△ABC中的∠A沿DE向下翻折，使点A落在点C处．若AE= ，则BC的长是 ．
18. 如图所示，点A是反比例函数y= 图象上一点，作AB⊥x轴，垂足为点B，若△AOB的面积为2，则k的值是 ．
三、解答题
-
19. 计算：（﹣1）2+（π﹣3.14）0﹣| ﹣2|
20. 先化简，再求值：（a﹣2b）（a+2b）﹣（a﹣2b）2+8b2 ， 其中a=﹣2，b= ．21. 如图所示，AB是⊙O的直径，点C为⊙O上一点，过点B作BD⊥CD，垂足为点D，连结BC．BC平分∠ABD．求证：CD为⊙O的切线．
22. 某校为选拔一名选手参加“美丽邵阳，我为家乡做代言”主题演讲比赛，经研究，按图所示的项目和权数对选拔赛参赛选手进行考评（因排版原因统计图不完整）．下表是李明、张华在选拔赛中的得分情况：项目
选手
服装
普通话
主题
演讲技巧
李明
85
70
80
85
张华
90
75
75
80
结合以上信息，回答下列问题：
(1)、求服装项目的权数及普通话项目对应扇形的圆心角大小；
(2)、求李明在选拔赛中四个项目所得分数的众数和中位数；
(3)、根据你所学的知识，帮助学校在李明、张华两人中选择一人参加“美丽邵阳，我为家乡做代言”主题演讲比赛，并说明理由．
23. 某公司计划购买A，B两种型号的机器人搬运材料．已知A型机器人比B型机器人每小时多搬运30kg材料，且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同．
(1)、求A，B两种型号的机器人每小时分别搬运多少材料；
(2)、该公司计划采购A，B两种型号的机器人共20台，要求每小时搬运材料不得少于2800kg，则至少购进A型机器人多少台？
24. 某商场为方便消费者购物，准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯．如图所示，已知原阶梯式自动扶梯AB长为10m，坡角∠ABD为30°；改造后的斜坡式自动扶梯的坡角∠ACB为15°，请你计算改造后的斜坡式自动扶梯AC的长度，（结果精确到0．lm．温馨提示：sin15°≈0.26，cosl5°≈0.97，tan15°≈0.27）
25. 如图1所示，在四边形ABCD中，点O，E，F，G分别是AB，BC，CD，AD的中点，连接OE，EF，FG，GO，GE．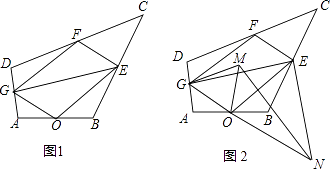
(1)、证明：四边形OEFG是平行四边形；
(2)、将△OGE绕点O顺时针旋转得到△OMN，如图2所示，连接GM，EN．①若OE= ，OG=1，求 的值；
②试在四边形ABCD中添加一个条件，使GM，EN的长在旋转过程中始终相等．（不要求证明）
26. 如图所示，将二次函数y=x2+2x+1的图象沿x轴翻折，然后向右平移1个单位，再向上平移4个单位，得到二次函数y=ax2+bx+c的图象．函数y=x2+2x+1的图象的顶点为点A．函数y=ax2+bx+c的图象的顶点为点B，和x轴的交点为点C，D（点D位于点C的左侧）．
(1)、求函数y=ax2+bx+c的解析式；(2)、从点A，C，D三个点中任取两个点和点B构造三角形，求构造的三角形是等腰三角形的概率；
(3)、若点M是线段BC上的动点，点N是△ABC三边上的动点，是否存在以AM为斜边的Rt△AMN，使△AMN的面积为△ABC面积的 ？若存在，求tan∠MAN的值；若不存在，请说明理由．