湖北省随州市2018年中考数学试卷
试卷更新日期:2018-08-03 类型:中考真卷
一、选择题
-
1. ﹣ 的相反数是( )
A、﹣ B、 C、﹣2 D、22. 如图是一个由4个相同正方体组成的立体图形,它的左视图是( )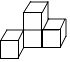 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列运算正确的是( )
3. 下列运算正确的是( )
A、a2•a3=a6 B、a3÷a﹣3=1 C、(a﹣b)2=a2﹣ab+b2 D、(﹣a2)3=﹣a64. 如图,在平行线l1、l2之间放置一块直角三角板,三角板的锐角顶点A,B分别在直线l1、l2上,若∠l=65°,则∠2的度数是( ) A、25° B、35° C、45° D、65°5. 某同学连续6次考试的数学成绩分别是85,97,93,79,85,95,则这组数据的众数和中位数分别为( )
A、25° B、35° C、45° D、65°5. 某同学连续6次考试的数学成绩分别是85,97,93,79,85,95,则这组数据的众数和中位数分别为( )
A、85 和 89 B、85 和 86 C、89 和 85 D、89 和 866. 如图,平行于BC的直线DE把△ABC分成面积相等的两部分,则 的值为( ) A、1 B、 C、 -1 D、 +17. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是( )A、
A、1 B、 C、 -1 D、 +17. “龟兔赛跑”这则寓言故事讲述的是比赛中兔子开始领先,但它因为骄傲在途中睡觉,而乌龟一直坚持爬行最终赢得比赛,下列函数图象可以体现这一故事过程的是( )A、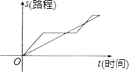 B、
B、 C、
C、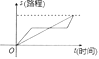 D、
D、 8. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )
8. 正方形ABCD的边长为2,以各边为直径在正方形内画半圆,得到如图所示阴影部分,若随机向正方形ABCD内投一粒米,则米粒落在阴影部分的概率为( )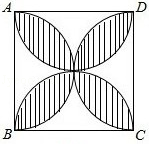 A、 B、 C、 D、9. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
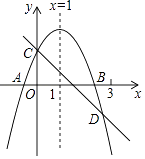
A、 B、 C、 D、9. 我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )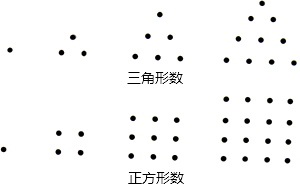 A、33 B、301 C、386 D、57110. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:
A、33 B、301 C、386 D、57110. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A、B两点,与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax2+bx+c交于C、D两点,D点在x轴下方且横坐标小于3,则下列结论:①2a+b+c>0;②a﹣b+c<0;③x(ax+b)≤a+b;④a<﹣1.
其中正确的有( )
 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 计算: ﹣|2﹣2 |+2tan45°= .
12. 如图,点A,B,C在⊙O上,∠A=40度,∠C=20度,则∠B=度.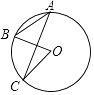 13. 已知 是关于x,y的二元一次方程组 的一组解,则a+b= .
13. 已知 是关于x,y的二元一次方程组 的一组解,则a+b= .
14. 如图,一次函数y=x﹣2的图象与反比例函数y= (k>0)的图象相交于A、B两点,与x轴交与点C,若tan∠AOC= ,则k的值为 . 15. 如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为 .
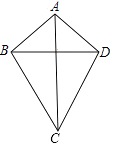
15. 如图,在平面直角坐标系xOy中,菱形OABC的边长为2,点A在第一象限,点C在x轴正半轴上,∠AOC=60°,若将菱形OABC绕点O顺时针旋转75°,得到四边形OA′B′C′,则点B的对应点B′的坐标为 . 16. 如图,在四边形ABCD中,AB=AD=5,BC=CD且BC>AB,BD=8.给出以下判断:
16. 如图,在四边形ABCD中,AB=AD=5,BC=CD且BC>AB,BD=8.给出以下判断:①AC垂直平分BD;②四边形ABCD的面积S=AC•BD;③顺次连接四边形ABCD的四边中点得到的四边形可能是正方形;④当A,B,C,D四点在同一个圆上时,该圆的半径为 ;⑤将△ABD沿直线BD对折,点A落在点E处,连接BE并延长交CD于点F,当BF⊥CD时,点F到直线AB的距离为 .其中正确的是 . (写出所有正确判断的序号)
三、解答题
-
17. 先化简,再求值: ,其中x为整数且满足不等式组 .
18. 已知关于x的一元二次方程x2+(2k+3)x+k2=0有两个不相等的实数根x1 , x2 .
(1)、求k的取值范围;(2)、若 =﹣1,求k的值.
19. 为了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘成如图所示的频数分布直方图,已知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题: (1)、图中a的值为;
(1)、图中a的值为;
(2)、若要绘制该样本的扇形统计图,则成绩x在“70≤x<80”所对应扇形的圆心角度数为度;
(3)、此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,则获得“优秀“的学生大约有人:
(4)、在这些抽查的样本中,小明的成绩为92分,若从成绩在“50≤x<60”和“90≤x<100”的学生中任选2人,请用列表或画树状图的方法,求小明被选中的概率.20. 随州市新㵐水一桥(如图1)设计灵感来源于市花﹣﹣兰花,采用蝴蝶兰斜拉桥方案,设计长度为258米,宽32米,为双向六车道,2018年4月3日通车.斜拉桥又称斜张桥,主要由索塔、主梁、斜拉索组成.某座斜拉桥的部分截面图如图2所示,索塔AB和斜拉索(图中只画出最短的斜拉索DE和最长的斜拉索AC)均在同一水平面内,BC在水平桥面上.已知∠ABC=∠DEB=45°,∠ACB=30°,BE=6米,AB=5BD. (1)、求最短的斜拉索DE的长;(2)、求最长的斜拉索AC的长.21. 如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.
(1)、求最短的斜拉索DE的长;(2)、求最长的斜拉索AC的长.21. 如图,AB是⊙O的直径,点C为⊙O上一点,CN为⊙O的切线,OM⊥AB于点O,分别交AC、CN于D、M两点.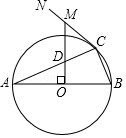 (1)、求证:MD=MC;(2)、若⊙O的半径为5,AC=4 ,求MC的长.22. 为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:
(1)、求证:MD=MC;(2)、若⊙O的半径为5,AC=4 ,求MC的长.22. 为迎接“世界华人炎帝故里寻根节”,某工厂接到一批纪念品生产订单,按要求在15天内完成,约定这批纪念品的出厂价为每件20元,设第x天(1≤x≤15,且x为整数)每件产品的成本是p元,p与x之间符合一次函数关系,部分数据如表:天数(x)
1
3
6
10
每件成本p(元)
7.5
8.5
10
12
任务完成后,统计发现工人李师傅第x天生产的产品件数y(件)与x(天)满足如下关系:y= ,
设李师傅第x天创造的产品利润为W元.
(1)、直接写出p与x,W与x之间的函数关系式,并注明自变量x的取值范围:(2)、求李师傅第几天创造的利润最大?最大利润是多少元?
(3)、任务完成后.统计发现平均每个工人每天创造的利润为299元.工厂制定如下奖励制度:如果一个工人某天创造的利润超过该平均值,则该工人当天可获得20元奖金.请计算李师傅共可获得多少元奖金?
23. 我们知道,有理数包括整数、有限小数和无限循环小数,事实上,所有的有理数都可以化为分数形式(整数可看作分母为1的分数),那么无限循环小数如何表示为分数形式呢?请看以下示例:例:将 化为分数形式
由于 =0.777…,设x=0.777…①
则10x=7.777…②
②﹣①得9x=7,解得x= ,于是得 = .
同理可得 = , =1+ =1+ ,
根据以上阅读,回答下列问题:(以下计算结果均用最简分数表示)
(1)、 = , =;
(2)、将 化为分数形式,写出推导过程;
(3)、 = , =;(注: =0.315315…, =2.01818…)
(4)、(探索发现)
①试比较 与1的大小: 1(填“>”、“<”或“=”)②若已知 = ,则 = .
(注: =0.285714285714…)
24. 如图1,抛物线C1:y=ax2﹣2ax+c(a<0)与x轴交于A、B两点,与y轴交于点C.已知点A的坐标为(﹣1,0),点O为坐标原点,OC=3OA,抛物线C1的顶点为G.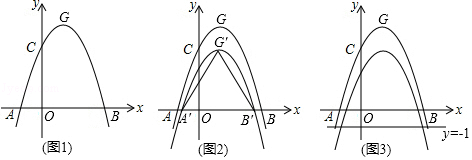 (1)、求出抛物线C1的解析式,并写出点G的坐标;(2)、如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2 , 设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(1)、求出抛物线C1的解析式,并写出点G的坐标;(2)、如图2,将抛物线C1向下平移k(k>0)个单位,得到抛物线C2 , 设C2与x轴的交点为A′、B′,顶点为G′,当△A′B′G′是等边三角形时,求k的值:
(3)、在(2)的条件下,如图3,设点M为x轴正半轴上一动点,过点M作x轴的垂线分别交抛物线C1、C2于P、Q两点,试探究在直线y=﹣1上是否存在点N,使得以P、Q、N为顶点的三角形与△AOQ全等,若存在,直接写出点M,N的坐标:若不存在,请说明理由.