2016-2017学年江苏省无锡市宜兴市丁蜀学区八年级上学期期中数学试卷
试卷更新日期：2017-02-17 类型：期中考试
一、选择题
-
1. 下列交通标志图案是轴对称图形的是（ ）A、
B、
C、
D、
2. 如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组（ ）A、3，4，5 B、5，12，13 C、12，15，25 D、 ， ，13. 下列各组图形中，一定是全等图形的是（ ）A、两个周长相等的等腰三角形 B、两个面积相等的长方形 C、两个斜边相等的直角三角形 D、两个周长相等的圆4. 已知等腰三角形的周长为15cm，一边长为7cm，则该等腰三角形的底边长为（ ）A、5 cm B、3cm或5 cm C、3 cm D、1 cm或7 cm5. 如图，在下列三角形中，若AB=AC，则能被一条直线分成两个小等腰三角形的是（ ）
A、（1）（2）（3） B、（1）（3）（4） C、（2）（3）（4） D、（1）（2）（4）6. 如图，∠AOB的平分线上一点P到OA的距离为5，Q是OB上任意一点，则（ ）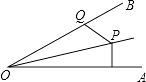
A、PQ≥5 B、PQ＞5 C、PQ≤5 D、PQ＜57. 如图，矩形ABCD中，AB=12cm，BC=24cm，如果将该矩形沿对角线BD折叠，那么图中阴影部分的面积（ ）cm2 ．
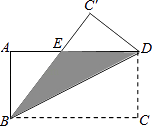A、72 B、90 C、108 D、1448. 如图，一圆柱高8cm，底面半径为 cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是（ ）
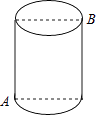A、6cm B、8cm C、10cm D、12cm二、填空题
-
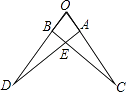
9. 已知等腰三角形的两边长是3cm和6cm，则这个等腰三角形的周长是 cm．10. 等腰三角形底边上的高线长5cm，则这个等腰三角形顶角的角平分线长 cm．11. 若直角三角形斜边长为6cm，则斜边上的中线长为 cm．12. 某直角三角形三条边的平方和为800，则这个直角三角形的斜边长为 ．13. 如图，△OAD≌△OBC，且∠O=72°，∠C=20°，则∠AEB=°．
14. 如图为某楼梯的侧面，测得楼梯的斜长AB为5米，高BC为3米，计划在楼梯表面铺地毯，地毯的长度至少需要米．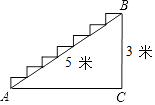
15. 如图，已知AC=FE，BC=DE，点A、D、B、F在一条直线上，要使△ABC≌△FDE，还需添加一个条件，这个条件可以是 ．
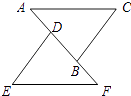16. 已知∠AOB=30°，点P在∠AOB内部且OP=4，P1与P关于OB对称，P2与P关于OA对称，则P1P2= ．17. 小河两岸边各有一棵树，分别高30尺和20尺，两树的距离是50尺，每棵树的树顶上都停着一只鸟．忽然，两只鸟同时看见水面上游出一条鱼，它们立刻飞去抓鱼，速度相同，并且同时到达目标．则这条鱼出现的地方离开比较高的树的距离为尺．18. 如图，在△ABC中，AB=AC=10，BC=12，若点P在边AC上移动，则BP的最小值是 ．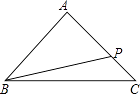
三、解答题
-
19. 如图：线段AD与BC相交于点O，且AC=BD，AD=BC．
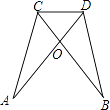
求证：
(1)、△ADC≌△BCD．(2)、CO=DO．20. 如图，在△ABC中，AB=AC，AC的垂直平分线分别交AB、AC于点D、E．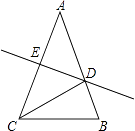
(1)、若∠A=40°，求∠DCB的度数．(2)、若AE=4，△DCB的周长为13，求△ABC的周长．21. 已知，如图，四边形ABCD中∠B=90°，AB=9，BC=12，AD=8，CD=17．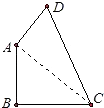
试求：
(1)、AC的长；(2)、四边形ABCD的面积．22. 解答题。(1)、如图，在“4×4”正方形网格中，已有2个小正方形被涂黑．请你分别在下面2张图中再若干个空白的小正方形涂黑，使得涂黑的图形成为轴对称图形．（图（1）要求只有1条对称轴，图（2）要求只有2条对称轴）．
(2)、在3×3的正方形格点图中，有格点△ABC和△DEF，且△ABC和△DEF关于某直线成轴对称，请在备用图中画出4个这样的△DEF．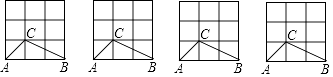
23. 如图，在Rt△ABC中，∠C=90°，∠BAC的角平分线AD交BC于点D，若AC=5，BC=12．求点D到AB的距离．
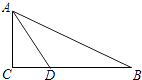24. 如图，牧童在A处放牛，其家在C处，A、C到河岸L的距离分别为AB=2km，CD=4km且，BD=8km．
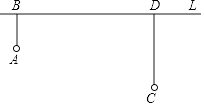(1)、牧童从A处将牛牵到河边P处饮水后再回到家C，试确定P在何处，所走路程最短？请在图中画出饮水的位置（保留作图痕迹），不必说明理由．
(2)、求出（1）中的最短路程．25. 如图，四边形ABCD，AD∥BC，∠B=90°，AD=6，AB=4，BC=9．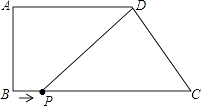
(1)、求CD的长为 ．(2)、点P从点B出发，以每秒1个单位的速度沿着边BC向点C运动，连接DP．设点P运动的时间为t秒，则当t为何值时，△PDC为等腰三角形？26.如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将一块三角板中含45°角的顶点放在A上，从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．
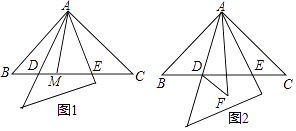(1)、小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；(2)、当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2 ． 同组的小颖和小亮随后想出了相同的方法进行解决：将△ABD沿AD所在的直线对折得到△ADF（如图2）；请证明小敏的发现的是正确的．