2016-2017学年湖南省张家界市桑植县八年级上学期期中数学试卷

试卷更新日期：2017-02-17 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各式： $\frac{a - b}{2}$ ， $\frac{x + 3}{x}$ ， $\frac{5 + y}{π}$ ， $\frac{a + b}{a - b}$ ， $\frac{1}{m}$ （x﹣y）中，是分式的共有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 若分式 $\frac{x^{2} - 4}{2 x - 4}$ 的值为零，则x等于（）

A、0 B、2 C、±2 D、﹣2

查看试题解析
3. 下列计算正确的是（）

A、 $\frac{3 y}{x} \div 3 x y = x^{2}$ B、 $\frac{3 y}{x^{2}}$ • $\frac{x}{3 y} = \frac{1}{x}$ C、x÷y• $\frac{1}{y} = x$ D、 $\frac{a}{a^{2}} - \frac{a - 1}{a} = \frac{1}{a + 1}$

查看试题解析
4. 已知a^m=2，aⁿ=3，则a^4m^﹣³ⁿ的值是（）

A、﹣ $\frac{16}{27}$ B、 $\frac{16}{27}$ C、﹣ $\frac{37}{16}$ D、 $\frac{27}{16}$

查看试题解析
5. 若△ABC≌△DEF，且△ABC的周长为20，AB=5，BC=8，则DF长为（）

A、5 B、8 C、7 D、5或8

查看试题解析
6. A，B两地相距48千米，一艘轮船从A地顺流航行至B地，又立即从B地逆流返回A地，共用去9小时，已知水流速度为4千米/时，若设该轮船在静水中的速度为x千米/时，则可列方程（）

A、 $\frac{48}{x + 4} + \frac{48}{x - 4} = 9$ B、 $\frac{48}{4 + x} + \frac{48}{4 - x} = 9$ C、 $\frac{48}{x}$ +4=9 D、 $\frac{96}{x + 4} + \frac{96}{x - 4} = 9$

查看试题解析
7. 若分式方程 $\frac{1}{x - 2} + 3 = \frac{a - x}{x - 2}$ 有增根，则a的值是（）

A、1 B、0 C、﹣1 D、3

查看试题解析
8. 有下列命题：①两点之间，线段最短； ②相等的角是对顶角； ③内错角互补，两直线平行．其中真命题的有（）

A、1个 B、2个 C、3个 D、0个

查看试题解析

二、填空题

9. 计算：（a^﹣²）³= ．

查看试题解析
10. 计算： $\frac{1}{x - 3}$ + $\frac{1}{3 - x}$ = ．

查看试题解析
11. 用科学记数法表示：﹣0.00002016= ．

查看试题解析
12. 如图，△ABC中，EF是AB的垂直平分线，与AB交于点D，BF=12，CF=3，则AC= ．

查看试题解析
13. 将命题“互为相反数的两个数之和等于零”写成：如果那么．

查看试题解析
14. 化简： $\frac{3 - x}{9 - 6 x + x^{2}}$ = ．

查看试题解析
15. 已知 $\frac{1}{x}$ ﹣ $\frac{1}{y}$ =3，则分式 $\frac{2 x + 3 y - 2 y}{x - 2 x y - y}$ 的值为．

查看试题解析
16. 等腰三角形的两边的长分别为5cm和7cm，则此三角形的周长是．

查看试题解析

三、解答题

17. 计算：

(1)、 ${(- \frac{1}{2})}^{- 1}$ ﹣2+（π﹣3.14）⁰

(2)、 $\frac{x^{2} - 1}{x^{2} + 2 x + 1}$ ÷ $\frac{x^{2} - x}{x + 1}$ ．

查看试题解析
18. 解下列分式方程：

(1)、 $\frac{3}{x} = \frac{2}{x - 1}$

(2)、 $\frac{3}{x + 1} + \frac{1}{x - 1} = \frac{6}{x^{2} - 1}$ ．

查看试题解析
19. 如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC．

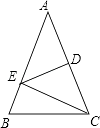(1)、求∠ECD的度数；

(2)、若CE=5，求BC长．

查看试题解析
20. 先化简，再求值： $\frac{a - 2}{a + 3} \div \frac{a^{2} - 4}{2 a + 6} - \frac{5}{a + 2}$ 选一个你所喜欢的数代入求值．

查看试题解析
21. 观察下面的变形规律：
$\frac{1}{1 \times 2}$ =1﹣ $\frac{1}{2}$ ； $\frac{1}{2 \times 3}$ = $\frac{1}{2}$ ﹣ $\frac{1}{3}$ ； $\frac{1}{3 \times 4}$ = $\frac{1}{3}$ ﹣ $\frac{1}{4}$ ；…解答下面的问题：

(1)、若n为正整数，请你猜想 $\frac{1}{n (n + 1)}$ =；

(2)、求和： $\frac{1}{1 \times 2}$ + $\frac{1}{2 \times 3}$ + $\frac{1}{3 \times 4}$ ．（注：只能用上述结论做才能给分）；

(3)、用上述相似的方法求和： $\frac{1}{1 \times 3}$ + $\frac{1}{3 \times 5}$ + $\frac{1}{5 \times 7}$ +…+ $\frac{1}{2013 \times 2015}$ ．

查看试题解析
22. 已知分式：A= $\frac{4}{x^{2} - 4}$ ，B= $\frac{1}{x + 2} + \frac{1}{2 - x}$ ，其中x≠±2．学生甲说A与B相等，乙说A与B互为倒数，丙说A与B互为相反数，她们三个人谁的结论正确？为什么？

查看试题解析
23. 去年入秋以来，某省发生了百年一遇的旱灾，连续8个多月无有效降水，为抗旱救灾，某部队计划为驻地村民新修水渠3600米，为了水渠能尽快投入使用，实际工作效率是原计划工作效率的1.8倍，结果提前20天完成修水渠任务．问原计划每天修水渠多少米？

查看试题解析
24. 解答题。

(1)、如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．
证明：DE=BD+CE．

(2)、如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

(3)、拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断△DEF的形状．

查看试题解析