2015-2016学年云南省曲靖市罗平县钟山一中八年级下学期期中数学试卷

试卷更新日期：2017-02-16 类型：期中考试

进入出卷网下载

一、选择题

1. 如果 $\sqrt{{(2 a - 1)}^{2}}$ =1﹣2a，则（）

A、a＜ $\frac{1}{2}$ B、a≤ $\frac{1}{2}$ C、a＞ $\frac{1}{2}$ D、a≥ $\frac{1}{2}$

查看试题解析
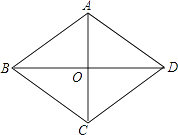
2. 下列计算正确的是（）

A、4 $\sqrt{3} - 3 \sqrt{3} = 1$ B、 $\sqrt{2} + \sqrt{3} = 5$ C、2 $\sqrt{\frac{1}{2}}$ = $\sqrt{2}$ D、3 $+ 2 \sqrt{2} = 5 \sqrt{2}$

查看试题解析
3. 已知y= $\sqrt{4 - x} + \sqrt{x - 4} + 3$ ，则 $\frac{y}{x}$ 的值为（）

A、 $\frac{4}{3}$ B、﹣ $\frac{4}{3}$ C、 $\frac{3}{4}$ D、﹣ $\frac{3}{4}$

查看试题解析
4. 如图所示，已知四边形ABCD的对角线AC，BD相交于点O，则下列能判断它是正方形的条件是（）

A、AO=BO=CO=DO，AC⊥BD B、AC=BC=CD=DA C、AO=CO，BO=DO，AC⊥BD D、AB=BC，CD⊥DA

查看试题解析
5. 把直角三角形两直角边同时扩大到原来的2倍，则斜边扩大到原来的（）

A、2倍 B、4倍 C、3倍 D、5倍

查看试题解析
6. 矩形、菱形、正方形都具有的性质是（）．

A、对角线相等 B、对角线互相平分 C、对角线互相垂直 D、对角线平分对角

查看试题解析
7. 一架25米长的云梯，斜立在一竖直的墙上，这时梯脚距离墙底端7米．如果梯子的顶端沿墙下滑4米，那么梯脚将水平滑动（）

A、9米 B、15米 C、5米 D、8米

查看试题解析
8. 一个正方形的边长为3，则它的对角线长为（）

A、3 B、3 $\sqrt{2}$ C、 $\sqrt{6}$ D、2 $\sqrt{6}$

查看试题解析
9. 若a，b为实数，且|a+1|+ $\sqrt{b - 1}$ =0，则（ab）²⁰¹⁴的值是（）

A、0 B、1 C、﹣1 D、±1

查看试题解析
10. 已知 $\sqrt{x} + \frac{1}{\sqrt{x}} = a$ ，则 $x + \frac{1}{x}$ 的值为（）

A、a²﹣2 B、a² C、a²﹣4 D、不确定

查看试题解析

二、空题

11. 化简： $\sqrt{{(\sqrt{3} - 2)}^{2}}$ = ．

查看试题解析
12. 若二次根式 $\sqrt{2 - x}$ 有意义，则x的取值范围是．

查看试题解析
13. 已知直角三角形的两边的长分别是3和4，则第三边长为．

查看试题解析
14. 若1≤x≤5，化简 $\sqrt{{(x - 1)}^{2}}$ +|x﹣5|= ．

查看试题解析
15. 已知△ABC为等边三角形，BD为中线，延长BC至E，使CE=CD=1，连接DE，则DE= ．

查看试题解析
16. 如图所示，有一条小路穿过长方形的草地ABCD，若AB=60m，BC=84m，AE=100m，则这条小路的面积是 m² ．

查看试题解析
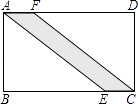17. 如图，有一圆柱体，它的高为8cm，底面周长为12cm．在圆柱的下底面A点处有一个蜘蛛，它想吃到上底面上与A点相对的B点处的苍蝇，需要爬行的最短路径是 cm．

查看试题解析
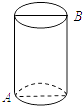18. 学校有一块长方形的花圃如右图所示，有少数的同学为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了步（假设1米=2步），却踩伤了花草，所谓“花草无辜，踩之何忍”！

查看试题解析
19. 如图，平行四边形ABCD中，对角线AC、BD相交于点O，AB=3，BC=5，则OA的取值范围为

查看试题解析
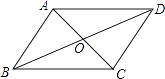20. 已知一个菱形的面积为8 $\sqrt{3}$ cm² ，且两条对角线的长度比为1： $\sqrt{3}$ ，则菱形的边长为．

查看试题解析

三、解答题

21. 计算（2 $- \sqrt{3}$ ²⁰¹³× ${(2 + \sqrt{3})}^{2014} + {(π - \sqrt{3})}^{0}$ +| $\sqrt{3}$ ﹣2|+9×3^﹣² ．

查看试题解析
22. 先化简，再求值 $\frac{a - b}{a}$ $\div (a - \frac{2 a b - b^{2}}{a})$ ，其中a= $\sqrt{3} + 1$ ，b= $\sqrt{3} - 1$ ．

查看试题解析
23. 计算：①（ ${(\sqrt{3} + \sqrt{2})}^{2}$ × $(5 - 2 \sqrt{6})$
② ${(\sqrt{3} - \sqrt{2})}^{2} + {(\sqrt{3} + \sqrt{2})}^{2}$ ．

查看试题解析
24. 已知x= $\frac{1}{2}$ （ $\sqrt{7}$ + $\sqrt{5}$ ），y= $\frac{1}{2}$ （ $\sqrt{7}$ ﹣ $\sqrt{5}$ ），则x²﹣xy+y²= ．

查看试题解析
25. 在实数范围内分解因式

(1)、x⁴﹣9

(2)、y²﹣2 $\sqrt{3}$ y+3．

查看试题解析
26. 麒麟区第七中学现有一块空地ABCD如图所示，现计划在空地上种草皮，经测量，∠B=90°，AB=3m，BC=4m，CD=13m，AD=12m．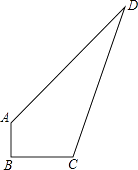

(1)、求出空地ABCD的面积？

(2)、若每种植1平方米草皮需要300元，问总共需投入多少元？

查看试题解析
27. 如图，▱ABCD中，点O是AC与BD的交点，过点O的直线与BA、DC的延长线分别交于点E、F．

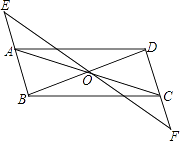(1)、求证：△AOE≌△COF；

(2)、请连接EC、AF，则EF与AC满足什么条件时，四边形AECF是矩形，并说明理由．

查看试题解析
28. 已知：如图，菱形花坛ABCD周长是80m，∠ABC=60°，沿着菱形的对角线修建了两条小路AC和BD，相交于O点．

(1)、求两条小路的长AC、BD．（结果可用根号表示）

(2)、求花坛的面积．（结果可用根号表示）

查看试题解析
29. 如图，在正方形ABCD中，E是AB上一点，F是AD延长线上一点，且DF=BE．

(1)、求证：CE=CF；

(2)、若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

查看试题解析