2015-2016学年四川省成都市成华区八年级下学期期中数学试卷
试卷更新日期:2017-02-16 类型:期中考试
一、选择题
-
1. 等腰三角形的顶角为100°,则它的一个底角是( )A、40° B、50° C、60° D、80°2. 如果a>b,那么下列各式中正确的是( )A、a﹣5<b﹣5 B、 < C、a+5<b+5 D、﹣3a<﹣3b3. 下列分解因式正确的是( )A、2x2+4xy=x(2x+4y) B、4a2﹣4ab+b2=2(a﹣b)2 C、x3﹣x=x(x2﹣1) D、3x2﹣5xy+x=x(3x﹣5y)4. 不等式组: 的解集在数轴上可表示为( )A、
 B、
B、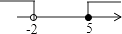 C、
C、 D、
D、 5. 如图,直线y=kx+b交坐标轴于A(﹣2,0)、B(0,3)两点,则不等式kx+b>0的解集是( )
5. 如图,直线y=kx+b交坐标轴于A(﹣2,0)、B(0,3)两点,则不等式kx+b>0的解集是( )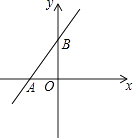 A、x>﹣2 B、x>3 C、x<﹣2 D、x<36. 下列各式不能用平方差公式法分解因式的是( )A、x2﹣4 B、﹣x2﹣y2+2xy C、m2n2﹣1 D、a2﹣4b27. 下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( )
A、x>﹣2 B、x>3 C、x<﹣2 D、x<36. 下列各式不能用平方差公式法分解因式的是( )A、x2﹣4 B、﹣x2﹣y2+2xy C、m2n2﹣1 D、a2﹣4b27. 下列美丽的图案,既是轴对称图形又是中心对称图形的个数是( ) A、1个 B、2个 C、3个 D、4个8. 如图,在以BC为底边的等腰△ABC中,∠A=30°,AC=8,则AC边上的高BD的长是( )
A、1个 B、2个 C、3个 D、4个8. 如图,在以BC为底边的等腰△ABC中,∠A=30°,AC=8,则AC边上的高BD的长是( ) A、4 B、8 C、2 D、49. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A、4 B、8 C、2 D、49. 如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )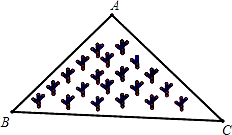 A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点10. 如图,在△ABC中,∠C=90°,AD是∠A角平分线,DE⊥AB于点E,CD=3,BC=8,则BE=( )
A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点10. 如图,在△ABC中,∠C=90°,AD是∠A角平分线,DE⊥AB于点E,CD=3,BC=8,则BE=( )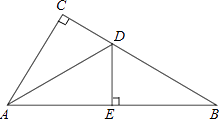 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
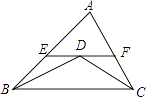
11. 已知a=2,x+2y=3,则3ax+6ay=12. 已知等腰三角形有两条边的长度分别是3和6,那么这个等腰三角形的周长是 .13. 如图,在△ABC中,AB=6cm,AC=4cm,BD平分∠ABC,CD平分∠ACB,EF过点D且EF∥BC,则△AEF的周长是 cm.
 14. 如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD=度.
14. 如图,在△ABC中,∠C=35°,AB=AD,DE是AC的垂直平分线,则∠BAD=度.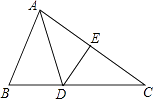 15. 小马用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,那么小马最多能买支钢笔.
15. 小马用100元钱去购买笔记本和钢笔共30件,已知每本笔记本2元,每支钢笔5元,那么小马最多能买支钢笔.三、解答题
-
16. 分解因式:(1)、2x2﹣18(2)、﹣3m+6m2﹣3m3 .17. 解不等式与不等式组(1)、求不等式 ﹣ ≤1的解集.(2)、解不等式组 ,把不等式组的解集在数轴上表示出来,并写出不等式组的非负整数解.18. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
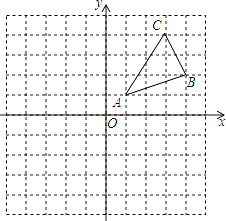
①画出△ABC向左平移5个单位长度后得到的△A1B1C1;
②请画出△ABC关于原点对称的△A2B2C2 , 并写出点A2、B2、C2坐标;
③请画出△ABC绕原点O逆时针旋转90°后△A3B3C3 , 并写出点A3、B3、C3坐标.
19. 学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.(1)、分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;(2)、问:该学校购买哪家制衣公司的服装比较合算?请说明理由.20. 如图,在△ABC中,∠C=90°,AC=BC,∠BAC的平分线AE交BC于点D,且AE⊥BE.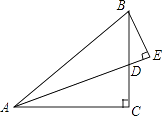 (1)、求∠DBE的大小;(2)、求证:AD=2BE.
(1)、求∠DBE的大小;(2)、求证:AD=2BE.四、填空题(二)
-
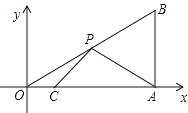
21. 分解因式:16a2﹣(a2+4)2= .22. 已知关于x的不等式组 的整数解有5个,则a的取值范围是23. 将一箱苹果分给若干个小朋友,若每位小朋友分5个苹果,则还剩12个苹果;若每位小朋友分8个苹果,则有一个小朋友能分到不足5个苹果.这一箱苹果的个数是 , 小朋友的人数是24. 如图,在平面直角坐标系中,Rt△OAB的顶点A在x轴的正半轴上,顶点B的坐标为(3, ),点C的坐标为( ,0),点P为斜边OB上的一动点,则PA+PC的最小值为
 25. 如图,在四个正方形拼接成的图形中,以A1、A2、A3、…、A10这十个点中任意三点为顶点,共能组成个等腰直角三角形.
25. 如图,在四个正方形拼接成的图形中,以A1、A2、A3、…、A10这十个点中任意三点为顶点,共能组成个等腰直角三角形.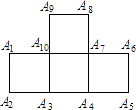
五、解答题(二)
-
26. 某工厂有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件,已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需用甲种原料4kg,乙种原料10kg,可获利润1200元.(1)、按要求安排A、B两种产品的生产件数,有哪几种方案?请你设计出来;(2)、设生产A、B两种产品总利润是W(元),采用哪种生产方案获总利润最大?最大利润为多少?27. 如图,点A的坐标是(﹣2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.
 (1)、求直线BD的函数表达式;(2)、求线段OF的长;(3)、连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.28. 如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ.
(1)、求直线BD的函数表达式;(2)、求线段OF的长;(3)、连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.28. 如图,在平面直角坐标系中,已知点A(0,2),△AOB为等边三角形,P是x轴上一个动点(不与原O重合),以线段AP为一边在其右侧作等边三角形△APQ. (1)、求点B的坐标;(2)、在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.(3)、连接OQ,当OQ∥AB时,求P点的坐标.
(1)、求点B的坐标;(2)、在点P的运动过程中,∠ABQ的大小是否发生改变?如不改变,求出其大小;如改变,请说明理由.(3)、连接OQ,当OQ∥AB时,求P点的坐标.