2015-2016学年江苏省镇江市八年级下学期期中数学试卷
试卷更新日期:2017-02-16 类型:期中考试
一、填空题
-
1. 当x时,分式 无意义.2. 在菱形ABCD中,如果∠A=60°,那么∠B=°.3. 调查某品牌洗衣机的使用寿命,采用的调查方式是 .4. 矩形是中心对称图形,对矩形ABCD而言,点A的对称点是点 .5. 约分: = .6. 一个样本的50个数据分别落在4个组内,第1、2、3组数据的个数分别是7、8、15,则第4组数据的频数与频率分别为7. 把一个正方形绕着其对称中点旋转一定的角度,要使旋转后的图形与原来的图形重合,那么旋转的角度至少是 .8. 如图,在▱ABCD中,BD为对角线,E、F分别是AD、BD的中点,连接EF.若EF=3,则CD的长为 .
 9. 如图,镇江四月份某日的温度变化情况,则这天中8时到18时的温差为
9. 如图,镇江四月份某日的温度变化情况,则这天中8时到18时的温差为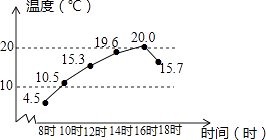 10. 如图,▱ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则▱ABCD的两条对角线长度之和为 .
10. 如图,▱ABCD的对角线交于点O,且AB=5,△OCD的周长为13,则▱ABCD的两条对角线长度之和为 .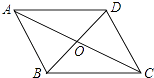 11. 如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为 .
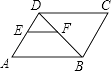
11. 如图,已知菱形ABCD的边长是13,O是对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.若菱形一条对角线长为10,则图中阴影部分的面积为 .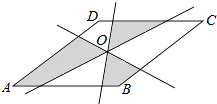 12. 如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN= .
12. 如图,在平行四边形ABCD中,AD=2AB,AH⊥CD于H,M为AD的中点,MN∥AB,连接NH,如果∠D=68°,则∠CHN= .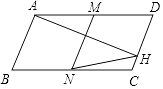
二、选择题.
-
13. 能清楚地表示出各部分在总体中所占百分比的统计图是( )A、条形统计图 B、扇形统计图 C、折线统计图 D、都可以14. 当x=1时,下列分式的值为0的是( )A、 B、 C、 D、15. 顺次连结矩形四边的中点所得的四边形是( )A、矩形 B、正方形 C、菱形 D、以上都不对16. 在硬地上掷1枚图钉,通常会出现两种情况:“钉尖着地”与“钉尖不着地”.任意重复抛掷1枚图钉很多次时,你认为是哪种情况的可能性大( )A、钉尖着地 B、钉尖不着地 C、一样大 D、不能确定17. 如图,□ABCD绕点A逆时针旋转32°,得到□AB′C′D′,若点B′与点B是对应点,若点B′恰好落在BC边上,则∠C=( )
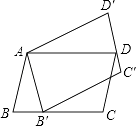 A、106° B、146° C、148° D、156°18. 如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )
A、106° B、146° C、148° D、156°18. 如图,由两个长为9,宽为3的全等矩形叠合而得到四边形ABCD,则四边形ABCD面积的最大值是( )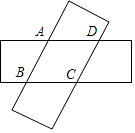 A、15 B、16 C、19 D、20
A、15 B、16 C、19 D、20三、解答题
-
19. 变形与求值(1)、通分: , .(2)、求值: ,其中x=1,y=﹣ .(3)、不改变分式的值,变形使分式 的分子与分母的最高次项的系数是正数.20. 如图,AD是△ABC的中线.
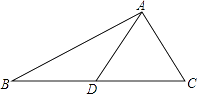 (1)、画图:延长AD到E,使ED=AD,连接BE、CE;(2)、四边形ABEC是平行四边形吗?证明你的结论.21. 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
(1)、画图:延长AD到E,使ED=AD,连接BE、CE;(2)、四边形ABEC是平行四边形吗?证明你的结论.21. 正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题: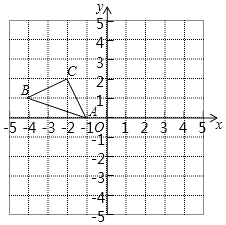 (1)、作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;(2)、点B1的坐标为 , 点C2的坐标为22. 某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.
(1)、作出△ABC绕点A逆时针旋转90°的△A1B1C1;作出△ABC关于原点O成中心对称的△A2B2C2;(2)、点B1的坐标为 , 点C2的坐标为22. 某学校开展课外球类特色的体育活动,决定开设A:羽毛球、B:篮球、C:乒乓球、D:足球四种球类项目.为了解学生最喜欢哪一种活动项目(每人只选取一种),随机抽取了部分学生进行调查,并将调查结果绘成如甲、乙所示的统计图,请你结合图中信息解答下列问题.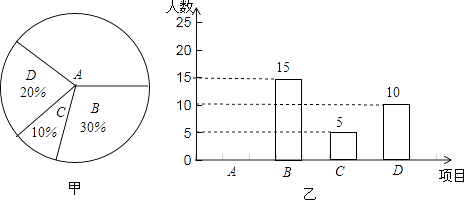 (1)、样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;(2)、请把条形统计图补充完整;(3)、若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?23. 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.
(1)、样本中最喜欢A项目的人数所占的百分比为 , 其所在扇形统计图中对应的圆心角度数是度;(2)、请把条形统计图补充完整;(3)、若该校有学生3000人,请根据样本估计全校最喜欢足球的学生人数约是多少?23. 如图,已知Rt△ABC中,∠ABC=90°,先把△ABC绕点B顺时针旋转90°至△DBE后,再把△ABC沿射线平移至△FEG,DE、FG相交于点H.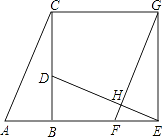 (1)、判断线段DE、FG的位置关系,并说明理由;(2)、连结CG,求证:四边形CBEG是正方形.24. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
(1)、判断线段DE、FG的位置关系,并说明理由;(2)、连结CG,求证:四边形CBEG是正方形.24. 在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(9)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:摸球的次数s
150
300
600
900
1200
1500
摸到白球的频数n
63
a
247
365
484
606
摸到白球的频率
0.420
0.410
0.412
0.406
0.403
b
(1)、按表格数据格式,表中的a=;b=;(2)、请估计:当次数s很大时,摸到白球的频率将会接近;(3)、请推算:摸到红球的概率是(精确到0.1);(4)、试估算:口袋中红球有多少只?(5)、解决了上面4个问题后,请你从统计与概率方面谈一条启示.25. 在△ABC中,AB=AC,点D是边BC所在的直线上的动点(点D不与B、C重合),过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.(1)、求证:AF=DE;(2)、若AC=5,DE=6,则DF= .(3)、试探究:D在不同位置时,DE,DF,AC具有怎样的数量关系,直接写出结论:①当点D在线段BC上时,关系是:;
②当点D在线段BC延长线上时,关系是:;
③当点D在线段CB延长线上时,关系是:;
(4)、请选择(3)中你探究获得的其中一个结论证明之.