江苏省南京市玄武区2018届九年级下学期数学测试试卷
试卷更新日期:2018-08-01 类型:中考模拟
一、单选题、
-
1. 2的相反数是( )A、 -2 B、2 C、- D、2. 下列运算正确的是( )A、2a+3b=5ab B、(-a2)3=a6 C、(a+b)2=a2+b2 D、2a2·3b2=6a2b23. 下列哪个几何体,它的主视图、左视图、俯视图都相同的是( )
A、 B、
B、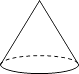 C、
C、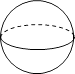 D、
D、 4. 如图,AB∥CD,直线EF与AB,CD分别交于点E,F,FG平分∠EFD,交AB于点G,若∠1=72°,则∠2的度数为( )
4. 如图,AB∥CD,直线EF与AB,CD分别交于点E,F,FG平分∠EFD,交AB于点G,若∠1=72°,则∠2的度数为( ) A、36° B、30° C、34° D、33°5. 已知二次函数y=x2-5x+m 的图像与 轴有两个交点,若其中一个交点的坐标为(1,0),则另一个交点的坐标为( )A、(-1,0) B、(4,0) C、(5,0) D、(-6,0)6. 如图,点A在反比例函数y= (x>0)的图像上,点B在反比例函数y= (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( )
A、36° B、30° C、34° D、33°5. 已知二次函数y=x2-5x+m 的图像与 轴有两个交点,若其中一个交点的坐标为(1,0),则另一个交点的坐标为( )A、(-1,0) B、(4,0) C、(5,0) D、(-6,0)6. 如图,点A在反比例函数y= (x>0)的图像上,点B在反比例函数y= (x>0)的图像上,AB∥x轴,BC⊥x轴,垂足为C,连接AC,若△ABC的面积是6,则k的值为( ) A、10 B、12 C、14 D、16
A、10 B、12 C、14 D、16二、填空题
-
7. 一组数据1,6,3,4,5的极差是 .8. 若式子 在实数范围内有意义,则x的取值范围是 .9. 国家统计局的相关数据显示,2017年我国国民生产总值约为830000亿元,用科学记数法表示830000是 .10. 分解因式x3-4x的结果是.11. 若关于x的一元二次方程x2-2x+a-1=0有实数根,则a的取值范围为 .12. 如图,在▱ABCD中,DB=DC,AE⊥BD,垂足为E,若∠EAB=46°,则∠C=°.
 13. 某圆锥的底面圆的半径为3cm,它的侧面展开图是半圆,则此圆锥的侧面积是cm2 . (结果保留π)14. 如图,在⊙O中,AE是直径,半径OD⊥弦AB,垂足为C,连接CE.若OC=3,△ACE的面积为12,则CD= .
13. 某圆锥的底面圆的半径为3cm,它的侧面展开图是半圆,则此圆锥的侧面积是cm2 . (结果保留π)14. 如图,在⊙O中,AE是直径,半径OD⊥弦AB,垂足为C,连接CE.若OC=3,△ACE的面积为12,则CD= . 15. 某商场销售一种商品,第一个月将此商品的进价提高20%作为销售价,共获利1200元,第二个月商场搞促销活动,将此商品的进价提高15%作为销售价,第二个月的销售量比第一个月增加了80件,并且商场第二个月比第一个月多获利300元.设此商品的进价是x元,则可列方程 .
15. 某商场销售一种商品,第一个月将此商品的进价提高20%作为销售价,共获利1200元,第二个月商场搞促销活动,将此商品的进价提高15%作为销售价,第二个月的销售量比第一个月增加了80件,并且商场第二个月比第一个月多获利300元.设此商品的进价是x元,则可列方程 .
16. 如图,在△ABC中,∠C=90°,AC=8,BC=6,点D是AB的中点,点E在边AC上,将△ADE沿DE翻折,使点A落在点A′处,当A′E⊥AC时,A′B= .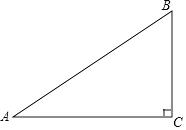
三、解答题
-
17.(1)、计算 -2sin45°+(2-π)0- ;(2)、解方程 x2-2x-1=0.18. 先化简,再求值: ,其中x= +1.19. 如图,在▱ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连接AE、CF.
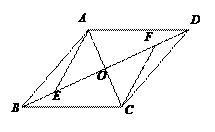 (1)、求证△AOE≌△COF;(2)、若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.20. 某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
(1)、求证△AOE≌△COF;(2)、若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.20. 某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表: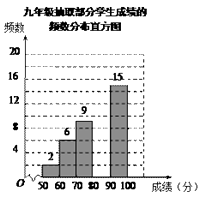

请根据所给信息,解答下列问题:
(1)、a= , b=;
(2)、请补全频数分布直方图;
(3)、已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,估计该年级成绩为优的有多少人?
21. 甲、乙两名同学参加1 000米比赛,由于参赛选手较多,将选手随机分A、B、C三组进行比赛.(1)、甲同学恰好在A组的概率是;(2)、求甲、乙两人至少有一人在B组的概率.22. 如图,将△ABC沿BC方向平移到△DEF,DE交AC于点G.若BC=2,△GEC的面积是△ABC的面积的一半,求△ABC平移的距离. 23. 一辆货车从甲地出发以50km/h的速度匀速驶往乙地,行驶1h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.
23. 一辆货车从甲地出发以50km/h的速度匀速驶往乙地,行驶1h后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.轿车行驶0.8h后两车相遇.图中折线ABC表示两车之间的距离y(km)与货车行驶时间x(h)的函数关系.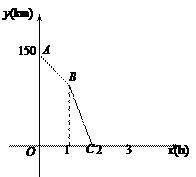 (1)、甲乙两地之间的距离是km,轿车的速度是km/h;(2)、求线段BC所表示的函数表达式;(3)、在图中画出货车与轿车相遇后的y(km)与x(h)的函数图象.24. 如图,甲楼AB高20m,乙楼CD高10m,两栋楼之间的水平距离BD=20m,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.
(1)、甲乙两地之间的距离是km,轿车的速度是km/h;(2)、求线段BC所表示的函数表达式;(3)、在图中画出货车与轿车相遇后的y(km)与x(h)的函数图象.24. 如图,甲楼AB高20m,乙楼CD高10m,两栋楼之间的水平距离BD=20m,小丽在乙楼楼顶C处观测电视塔塔顶E,测得仰角为45°,求电视塔的高度EF.(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75, ≈1.4,结果保留整数)
 25. 如图,在四边形ABCD中,AB=AD,∠C=90°,以AB为直径的⊙O交AD于点E,CD=ED,连接BD交⊙O于点F.
25. 如图,在四边形ABCD中,AB=AD,∠C=90°,以AB为直径的⊙O交AD于点E,CD=ED,连接BD交⊙O于点F. (1)、求证:BC与⊙O相切;(2)、若BD=10,AB=13,求AE的长.26. 甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.
(1)、求证:BC与⊙O相切;(2)、若BD=10,AB=13,求AE的长.26. 甲、乙两公司同时销售一款进价为40元/千克的产品.图①中折线ABC表示甲公司销售价y1(元/千克)与销售量x(千克)之间的函数关系,图②中抛物线表示乙公司销售这款产品获得的利润y2(元)与销售量x(千克)之间的函数关系.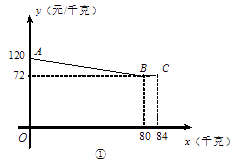
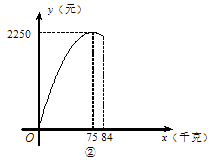 (1)、分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(1)、分别求出图①中线段AB、图②中抛物线所表示的函数表达式;
(2)、当该产品销售量为多少千克时,甲、乙两公司获得的利润的差最大?最大值为多少?