江苏省南京市联合体2018届数学中考一模试卷

试卷更新日期：2018-08-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算│－5＋3│的结果是（）

A、－8 B、8 C、－2 D、2

查看试题解析
2. 计算(－xy²)³的结果是（）

A、－x³y⁶ B、x³y⁶ C、x⁴y⁵ D、－x⁴y⁵

查看试题解析
3. 中国是严重缺水的国家之一．若每人每天浪费的水量为0.4 L，那么8 000 000人每天浪费的水量用科学记数法表示为（）

A、3.2×10⁸L B、3.2×10⁷L C、3.2×10⁶L D、3.2×10⁵L

查看试题解析
4. 如果m＝ $\sqrt{27}$ ，那么m的取值范围是（）

A、3＜m＜4 B、4＜m＜5 C、5＜m＜6 D、6＜m＜7

查看试题解析
5. 在平面直角坐标系中，点A的坐标是（1，3），将点A绕原点O顺时针旋转90°得到点A′，则点A′的坐标是（）

A、（－3，1） B、（3，－1） C、（－1，3） D、（1，－3）

查看试题解析
6. 如图，⊙O₁与⊙O₂的半径均为5，⊙O₁的两条弦长分别为6和8，⊙O₂的两条弦长均为7，则图中阴影部分面积的大小关系为（）

A、S₁＞S₂ B、S₁＜S₂ C、S₁＝S₂ D、无法确定

查看试题解析

二、填空题

7. 若式子 $\sqrt{x + 3}$ 在实数范围内有意义，则x的取值范围是．

查看试题解析
8. 计算（ $\sqrt{8}$ － $\sqrt{\frac{1}{2}}$ ）× $\sqrt{2}$ 的结果是．

查看试题解析
9. 分解因式3a²－6a＋3的结果是．

查看试题解析
10. 为了解居民用水情况，小明在某小区随机抽查了20户家庭的月用水量，结果如下表：
月用水量（m³）
4
5
6
8
9
户数
4
6
5
4
1

(1)、则这20户家庭的月用水量的众数是m³ ，中位数是m³ ．

查看试题解析
11. 已知方程 $x^{2} - x - 3 = 0$ 的两根是 $x_{1}$ ， $x_{2}$ ，则 $x_{1} + x_{2} =$ ， $x_{1} x_{2} =$ ．

查看试题解析
12. 函数y＝ $\frac{k_{1}}{x}$ 与y＝k₂x（k₁、k₂均是不为0的常数，）的图像交于A、B两点，若点A的坐标是（2，3），则点B的坐标是．

查看试题解析
13. 如图，在△ABC中，AC＝BC，把△ABC沿AC翻折，点B落在点D处，连接BD，若∠CBD＝16°，则∠BAC＝°．

查看试题解析
14. 如图，在⊙O的内接五边形ABCDE中，∠B＋∠E＝210°，则∠CAD＝°．

查看试题解析
15. 如图，在四边形ABCD中，AD∥BC (BC＞AD)，∠D＝90°，∠ABE＝45°，BC＝CD，
若AE＝5，CE=2，则BC的长度为．

查看试题解析

三、解答题

16. 解不等式组 ${\begin{matrix} 3 x + 2 > x \\ 2 (x + 1) \geq 4 x - 1 \end{matrix}$ .

查看试题解析
17. 先化简，再求值： $(\frac{1}{a + 2} - 1) \div \frac{a^{2} - 1}{a + 2}$ ，其中a=-3．

查看试题解析
18. 某厂为支援灾区人民，要在规定时间内加工1500顶帐篷．在加工了300顶帐篷后，厂家把工作效率提高到原来的1.5倍，结果提前4天完成任务，求该厂原来每天加工多少顶帐篷？

查看试题解析

19. 城南中学九年级共有12个班，每班48名学生，学校对该年级学生数学学科学业水平测试成绩进行了抽样分析，请按要求回答下列问题：

(1)、【收集数据】要从九年级学生中抽取一个48人的样本，你认为以下抽样方法中最合理的是．
①随机抽取一个班级的48名学生；②在九年级学生中随机抽取48名女学生；③在九年级12个班中每班各随机抽取4名学生．

(2)、【整理数据】将抽取的48名学生的成绩进行分组，绘制成绩频数分布表和成绩分布扇形统计图如下．

请根据图表中数据填空：

①表中m的值为；

② B类部分的圆心角度数为°；

③估计C、D类学生大约一共有名．

九年级学生数学成绩频数分布表

成绩（单位：分）	频数	频率
A类（80～100）	24	$\frac{1}{2}$
B类（60～79）	12	$\frac{1}{4}$
C类（40～59）	8	m
D类（0～39）	4	$\frac{1}{12}$

(3)、【分析数据】教育主管部们为了解学校学生成绩情况，将同层次的城南、城北两所中学的抽样数据进行对比分析，得到下表：

学校	平均数（分）	方差	A、B类的频率和
城南中学	71	358	0.75
城北中学	71	588	0.82

请你评价这两所学校学生数学学业水平测试的成绩，提出一个解释来支持你的观点．

查看试题解析

20. 甲、乙、丙三人到某商场购物，他们同时在该商场的地下车库等电梯，三人都任意从1至3层的某一层出电梯．

(1)、求甲、乙两人从同一层楼出电梯的概率；

(2)、甲、乙、丙三人从同一层楼出电梯的概率为.

查看试题解析
21. 如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．

(1)、求证：△AEF≌△DEB；

(2)、若∠BAC=90°，求证：四边形ADCF是菱形．

查看试题解析
22. 如图，在建筑物AB上，挂着35 m长的宣传条幅AE，从另一建筑物CD的顶部D处看条幅顶端A处，仰角为45°，看条幅底端E处，俯角为37°．求两建筑物间的距离BC．
(参考数据：sin37°≈0.6，cos37°≈0.8， tan37°≈0.75)

查看试题解析
23. 已知二次函数y＝ax²＋bx＋c中，函数y与自变量x的部分对应值如下表：
x
…
－1
0
1
2
3
…
y
…
8
3
0
－1
0
…

(1)、当ax²＋bx＋c＝3时，则 x＝；

(2)、求该二次函数的表达式；

(3)、将该函数的图象向上（下）平移，使图像与直线y＝3只有一个公共点，直接写出平移后的函数表达式．

查看试题解析
24. 如图，在半径为3的⊙O中，AB是直径，AC是弦，且AC＝4 $\sqrt{2}$ ．过点O作直径DE⊥AC，垂足为点P，过点B的直线交AC的延长线和DE的延长线于点F、G．

(1)、求线段AP、CB的长；

(2)、若OG＝9，求证：FG是⊙O的切线．

查看试题解析
25. 如图①，点A表示小明家，点B表示学校．小明妈妈骑车带着小明去学校，到达C处时发现数学书没带，于是妈妈立即骑车原路回家拿书后再追赶小明，同时小明步行去学校，到达学校后等待妈妈．假设拿书时间忽略不计，小明和妈妈在整个运动过程中分别保持匀速．妈妈从C处出发x分钟时离C处的距离为y₁米，小明离C处的距离为y₂米，如图②，折线O-D-E-F表示y₁与x的函数图象；折线O-G-F表示y₂与x的函数图象．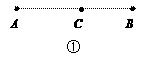

(1)、小明的速度为m/min，图②中a的值为．

(2)、设妈妈从C处出发x分钟时妈妈与小明之间的距离为y米．
①写出小明妈妈在骑车由C处返回到A处的过程中，y与x的函数表达式及x的取值范围；
②在图③中画出整个过程中y与x的函数图象．（要求标出关键点的坐标）

查看试题解析
26. 如图①，矩形ABCD中，AB＝4，BC＝m（m＞1），点E是AD边上一定点，且AE＝1．

(1)、当m＝3时，AB上存在点F，使△AEF与△BCF相似，求AF的长度．

(2)、如图②，当m＝3.5时．用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F．（不写作法，保留作图痕迹）

(3)、对于每一个确定的m的值，AB上存在几个点F，使得△AEF与△BCF相似？

查看试题解析

月用水量（m³）	4	5	6	8	9
户数	4	6	5	4	1

x	…	－1	0	1	2	3	…
y	…	8	3	0	－1	0	…