河南省重点中学2018届中考数学内部模拟试卷

试卷更新日期：2018-08-01 类型：中考模拟

进入出卷网下载

一、单选题

1. $\sqrt{9}$ 的算术平方根是（）

A、3 B、 $\sqrt{3}$ C、±3 D、± $\sqrt{3}$

查看试题解析
2. 据统计，大数据市场规模2020年预计达到10270亿元，将数据10270亿用科学记数法表示为（）

A、1.0270×10⁹ B、0.10270×10¹⁰ C、10.270×10¹¹ D、1.0270×10¹²

查看试题解析
3. 如图所示的几何体，其左视图是（）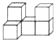

A、 B、 C、 D、

查看试题解析
4. 计算（x﹣2）^x=1，则x的值是（）

A、3 B、1 C、0 D、3或0

查看试题解析
5. 下表是某校“河南省汉子听写大赛初赛”冠军组成员的年龄分布
年龄/岁
12
13
14
15
人数
5
15
x
12﹣x
对于不同的x，下列关于年龄的统计量不会发生改变的是（）

A、平均数、中位数 B、平均数、方差 C、众数、中位数 D、中位数、方差

查看试题解析
6. 如果一次函数y=kx+b（k、b是常数）的图象不经过第二象限，那么k、b应满足的条件是（）

A、k＞0，且b≤0 B、k＜0，且b＞0 C、k＞0，且b≥0 D、k＜0，且b＜0

查看试题解析
7. 如图所示，△ABC中，已知AB=7，∠C=90°，∠B=60°，MN是中位线，则MN的长为（）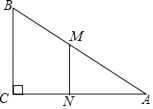

A、2 B、 $\frac{7}{4}$ C、2 $\sqrt{3}$ D、2 $\sqrt{5}$

查看试题解析
8. 九（1）班男生参加体育加试，经抽签分为①②③三个小组，已知小明不在①组，小华不在③组，那么小明与小华分在同一组的概率是（）

A、 $\frac{1}{8}$ B、 $\frac{1}{6}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
9. 如图所示，有一个半径为2的扇形，∠AOB=90°，其中OC平分∠AOB，BE⊥OC，CD⊥AO，则图中阴影面积为（）

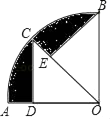A、π﹣1 B、π﹣2 C、 $\frac{3 π}{4}$ ﹣2 D、 $\frac{2 π}{3}$ ﹣1

查看试题解析
10. 已知抛物线：y=ax²+bx+c（a＜0）经过A（2，4）、B（﹣1，1）两点，顶点坐标为（h，k），则下列正确结论的序号是（）
①b＞1；②c＞2；③h＞ $\frac{1}{2}$ ；④k≤1．

A、①②③④ B、①②③ C、①②④ D、②③④

查看试题解析

二、填空题

11. 计算： $\sqrt{72} - 2 \sqrt{\frac{1}{2}}$ 等于．

查看试题解析
12. 不等式组 ${\begin{matrix} x - 1 \leq 3 \\ 2 x + 3 > 5 \end{matrix}$ 的解集是．

查看试题解析
13. 已知函数y= $\frac{4}{x}$ 与y=﹣x+5的图象的交点坐标为（a，b），则 $\frac{1}{a} + \frac{1}{b}$ 的值为．

查看试题解析
14. 如图所示，一次函数y=k₁x+3（k₁＜0）的图象与反比例函数y= $\frac{k_{2}}{x}$ （k₂＞0）的图象交于M、N两点，过点M作MC⊥y轴于点C，已知CM=1，则k₁﹣k₂= ．

查看试题解析
15. 在等腰△ABC中，AB=AC=8，BC=6，将△ABC的一角沿着MN折叠，点B'落在AC上，若△ABC与△B'MC相似，则BM的长度为．

查看试题解析

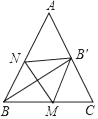
三、解答题

16. 化简（ $\frac{x + 2}{1 - x^{2}} - \frac{2}{x + 1}$ ）÷ $\frac{x}{1 - x}$ ，并在﹣1，0，1，2中选出一个合适的数代入求值．

查看试题解析
17. 中考科目已经发生变革，继中考增加体育实验之后，从2019年开始河南中考开始增设生物和地理科目，针对于此学校教务处王老师负责调查学生对此变革是否有压力，设置问题答案如下（A：大，B：一般，C：无），再将调查结果制成两幅不完统计图（如图所示），请根据统计图解答下列问题：

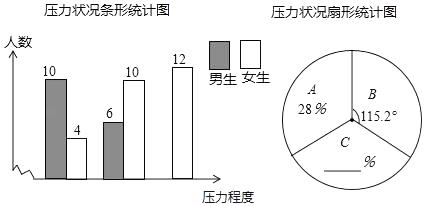(1)、本次调查中，王老师一共调查了名学生；

(2)、将条形统计图和扇形统计图补充完整；

(3)、为了缓解学生压力，王老师从被调查的A类和B类学生中分别选取一名学生进行详细心理调查，请用合适的方法恰好选中一名男生和一名学生的概率．

查看试题解析
18. 如图所示，点ABD都在⊙O上，BC是⊙O的切线，AD∥BC，∠C=30°，AD=4 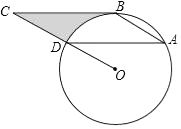$\sqrt{3}$ ．

(1)、求∠A的度数；

(2)、求由线段BC、CD与弧BD所围成的阴影部分的面积．（结果保留π）

查看试题解析
19. 2018年年初，某小区应辖区派出所要求在广场树立一个“打黑除恶，共创和谐”的矩形电子灯牌，如图所示，施工人员在两侧加固合金框架，已知合金框架底端G距广告牌立柱距离FD为4米，从G点测得广告牌顶端F点和底端E点的仰角分别是60°和45°．

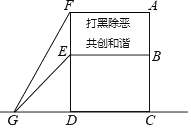(1)、若AF长为5米，求灯牌的面积；

(2)、求两侧加固的铝合金框架总共用料多少米？（本题中的计算过程和结果均保留根号）

查看试题解析
20. 如图所示，已知矩形ABOC中，AC=4，双曲线y= $\frac{6}{x}$ 与矩形两边AB、AC分别交于D、E，E为AC边中点．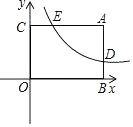

(1)、求点E的坐标；

(2)、点P是线段OB上的一个动点，是否存在点P，使∠DPC=90°？若存在，求出此时点P的坐标，若不存在，请说明理由．

查看试题解析
21. 某F2C直营店招牌：“新进最新款洗发水40瓶，每件售价80元，若一次性购买不超过10瓶时，售价不变；若一次性购买超过10瓶时，每多买1瓶，所买的每瓶洗发水的售价均降低2元．”已知该瓶洗发水每瓶进价52元，设顾客一次性购买洗发水x瓶时，他所付洗发水单价y元，该直营店所获利润为W元．

(1)、求y与x的函数关系式，并写出自变量x的取值范围；

(2)、顾客一次性购买多少瓶时，该直营店从中获利最多？

查看试题解析
22. 如图所示，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，EC的延长线交BD于点P．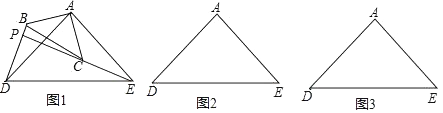

(1)、把△ABC绕点A旋转到图1，BD，CE的关系是（选填“相等”或“不相等”）；简要说明理由；

(2)、若AB=3，AD=5，把△ABC绕点A旋转，当∠EAC=90°时，在图2中作出旋转后的图形，求PD的值，简要说明计算过程；

(3)、在（2）的条件下写出旋转过程中线段PD的最小值为，最大值为．

查看试题解析
23. 如图所示，在平面直角坐标系中，矩形AOBC的两边与坐标轴重合，且OB=4，AO=3，若AD=3DC，以D为顶点的抛物线过原点．点M、N为动点，设运动时间为t秒．

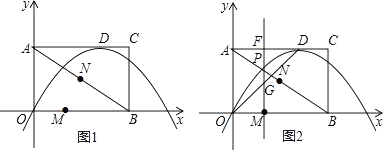(1)、求抛物线的解析式；

(2)、在图1中，若点M在线段OB上从点O向点B以1个单位/秒的速度运动，同时，点N在线段BA上从点B向点A以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△BMN为直角三角形？

(3)、在图2中，过点M做y轴的平行线，分别交抛物线和线段OD于P、G两点，当t为何值时，△ODP的面积最大？最大值是多少？

查看试题解析

年龄/岁	12	13	14	15
人数	5	15	x	12﹣x