河南省信阳市2018届九年级数学中考一模试卷
试卷更新日期:2018-08-01 类型:中考模拟
一、单选题、
-
1. –23的相反数是( )A、–8 B、8 C、–6 D、62. 碳纳米管的硬度与金刚石相当,却拥有良好的柔韧性,可以拉伸,我国某物理所研究组已研制出直径为0.5纳米的碳纳米管,1纳米=0.000000001米,则0.5纳米用科学记数法表示为( )
A、0.5×10–9米 B、5×10–8米 C、5×10–9米 D、5×10–10米3. 如图是一个几何体的三视图,则这个几何体是( ) A、
A、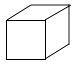 B、
B、 C、
C、 D、
D、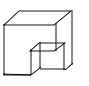 4. 下列计算正确的是( )A、a6÷a2=a3 B、a•a4=a4 C、(a3 )4=a7 D、(﹣2a )﹣2=5. 如图是边长为10 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位: )不正确的( )
4. 下列计算正确的是( )A、a6÷a2=a3 B、a•a4=a4 C、(a3 )4=a7 D、(﹣2a )﹣2=5. 如图是边长为10 的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位: )不正确的( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
6. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:尺码
39
40
41
42
43
平均每天销售数量/件
10
12
20
12
12
该店主决定本周进货时,增加一些41码的衬衫,影响该店主决策的统计量是( )
A、平均数 B、方差 C、众数 D、中位数7. 如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )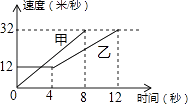 A、乙前4秒行驶的路程为48米 B、在0到8秒内甲的速度每秒增加4米/秒 C、两车到第3秒时行驶的路程相等 D、在4至8秒内甲的速度都大于乙的速度8.
A、乙前4秒行驶的路程为48米 B、在0到8秒内甲的速度每秒增加4米/秒 C、两车到第3秒时行驶的路程相等 D、在4至8秒内甲的速度都大于乙的速度8.如图,将矩形MNPQ放置在矩形ABCD中,使点M,N分别在AB,AD边上滑动,若MN=6,PN=4,在滑动过程中,点A与点P的距离AP的最大值为( )
 A、4 B、2 C、7 D、8
A、4 B、2 C、7 D、8二、填空题
-
9. 分解因式:x2y–xy2= .10. 不等式组 的最小整数解是 .11. 如图,在已知的△ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB= .
 12. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π).
12. 如图,在▱ABCD中,AD=2,AB=4,∠A=30°,以点A为圆心,AD的长为半径画弧交AB于点E,连接CE,则阴影部分的面积是(结果保留π). 13. 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2 ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为
13. 如图,在矩形ABCD中,AB=8,AD=6,点E为AB上一点,AE=2 ,点F在AD上,将△AEF沿EF折叠,当折叠后点A的对应点A'恰好落在BC的垂直平分线上时,折痕EF的长为
三、解答题
-
14. 化简并求值:(m+1)2+(m+1)(m﹣1),其中m是方程x2+x﹣1=0的一个根.15. 某中学初二年级抽取部分学生进行跳绳测试.并规定:每分钟跳90次以下的为不及格;每分钟跳90~99次的为及格;每分钟跳100~109次的为中等;每分钟跳110~119次的为良好;每分钟跳120次及以上的为优秀.测试结果整理绘制成如下两幅不完整的统计图.请根据图中信息,解答下列各题:
 (1)、参加这次跳绳测试的共有人;(2)、补全条形统计图;(3)、在扇形统计图中,“中等”部分所对应的圆心角的度数是;
(1)、参加这次跳绳测试的共有人;(2)、补全条形统计图;(3)、在扇形统计图中,“中等”部分所对应的圆心角的度数是;
(4)、如果该校初二年级的总人数是480人,根据此统计数据,请你估算该校初二年级跳绳成绩为“优秀”的人数.
16. 如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且CE=CB (1)、求证:BC是⊙O的切线;(2)、连接AF,BF,求∠ABF的度数.
(1)、求证:BC是⊙O的切线;(2)、连接AF,BF,求∠ABF的度数.
17. 共享单车被誉为“新四大发明”之一,如图1所示是某公司2017年向信阳市场提供一种共享自行车的实物图,车架档AC与CD的长分别为45cm,60cm,AC⊥CD,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.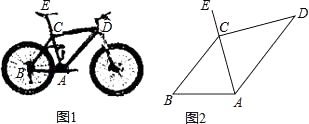 (1)、求车架档AD的长;(2)、求车座点E到车架档AB的距离.(结果精确到1cm,参考数据:sin75°=0.9659,cos75°=0.2588,tan75°=3.7321)18. 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=– x+3交AB,BC于点M,N,反比例函数 的图象经过点M,N.
(1)、求车架档AD的长;(2)、求车座点E到车架档AB的距离.(结果精确到1cm,参考数据:sin75°=0.9659,cos75°=0.2588,tan75°=3.7321)18. 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=– x+3交AB,BC于点M,N,反比例函数 的图象经过点M,N. (1)、求反比例函数的解析式;(2)、若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
19. 某班为参加学校的大课间活动比赛,准备购进一批跳绳,已知2根A型跳绳和1根B型跳绳共需56元,1根A型跳绳和2根B型跳绳共需82元.
(1)、求一根A型跳绳和一根B型跳绳的售价各是多少元?(2)、学校准备购进这两种型号的跳绳共50根,并且A型跳绳的数量不多于B型跳绳数量的3倍,请设计书最省钱的购买方案,并说明理由.
20.(1)、问题发现:
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为;
(2)、深入探究:如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)、拓展延伸:如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN= ,试求EF的长.
21. 如图,在矩形OABC中,点O为原点,边OA的长度为8,对角线AC=10,抛物线y= x2+bx+c经过点A、C,与AB交于点D. (1)、求抛物线的函数解析式;(2)、点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
(1)、求抛物线的函数解析式;(2)、点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.①求S关于m的函数表达式并求出S最大时的m值;
②在S最大的情况下,在抛物线y= x2+bx+c的对称轴上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.