河南省南阳市镇平县2018届数学中考一模试卷

试卷更新日期：2018-08-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 一个正方形的面积是15，估计它的边长大小在（　　）

A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间

查看试题解析
2. 如图，在直角坐标系中，有两点A(6，3)、B(6，0)．以原点O为位似中心，相似比为 $\frac{1}{3}$ ，在第一象限内把线段AB缩小后得到线段CD，则点C的坐标为（）

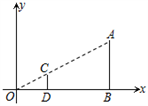A、(2，1) B、(2，0) C、(3，3) D、(3，1)

查看试题解析
3. 如图，⊙O是△ABC的外接圆，∠BOC＝120°，则∠BAC的度数是（）

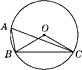A、70° B、60° C、50° D、30°

查看试题解析
4. 某种品牌运动服经过两次降价，每件零售价由560元降为315元，已知两次降价的百分率相同，求每次降价的百分率．设每次降价的百分率为x，下面所列的方程中正确的是（）

A、560(1＋x)²＝315 B、560(1－x)²＝315 C、560(1－2x)²＝315 D、560(1－x²)＝315

查看试题解析
5. 如图，正六边形ABCDEF内接于⊙O，半径为4，则这个正六边形的边心距OM的长为（）

A、2 B、2 $\sqrt{3}$ C、 $\sqrt{3}$ D、4 $\sqrt{3}$

查看试题解析
6. 四张相同的卡片，每张的正面分别写着 $\sqrt{5}$ ， $\sqrt{6}$ ， $\sqrt{7}$ ， $\sqrt{8}$ ，将卡片正面朝下扣在桌上，随机抽出一张，这张卡片上写的不是最简二次根式的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
7.
如图，△ABC中，cosB= $\frac{\sqrt{2}}{2}$ ，sinC= $\frac{3}{5}$ ，AC=5，则△ABC的面积是（）

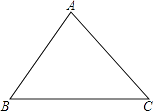A、 $\frac{21}{2}$ B、12 C、14 D、21

查看试题解析
8. 抛物线y=﹣x²+bx+c上部分点的横坐标x，纵坐标y的对应值如下表所示：
x
…
﹣2
﹣1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知，下列说法中，错误的是（）

A、抛物线于x轴的一个交点坐标为（﹣2，0） B、抛物线与y轴的交点坐标为（0，6） C、抛物线的对称轴是直线x=0 D、抛物线在对称轴左侧部分是上升的

查看试题解析
9. 某家庭搬进新居后又添置了新的电冰箱、电热水器等家用电器，为了了解用电量的大小，该家庭在6月份初连续几天观察电表的度数，电表显示的度数如下表：
日期
1日
2日
3日
4日
5日
6日
7日
8日
电表显示度数(度)
115
118
122
127
133
136
140
143
估计这个家庭六月份用电度数为（）

A、105度 B、108.5度 C、120度 D、124度

查看试题解析

二、填空题

10. 如图，一段抛物线：y=﹣x（x﹣2）（0≤x≤2）记为C₁ ，它与x轴交于两点O，A₁；将C₁绕A₁旋转180°得到C₂ ，交x轴于A₂；将C₂绕A₂旋转180°得到C₃ ，交x轴于A₃；…如此进行下去，直至得到C₆ ，若点P（11，m）在第6段抛物线C₆上，则m= ．

查看试题解析
11. 计算（ $\frac{5}{\sqrt{5}}$ ﹣2 $\sqrt{45}$ ）÷（﹣ $\sqrt{5}$ ）的结果为．

查看试题解析
12. 一个不透明的袋中装有除颜色外均相同的8个黑球、4个白球和若干个红球．每次摇匀后随机摸出一个球，记下颜色后再放回袋中，通过大量重复摸球试验后，发现摸到红球的频率稳定于0.4，由此可估计袋中约有红球个．

查看试题解析
13. 如图，AB是半圆O的直径，点C、D是半圆O的三等分点，若弦CD=2，则图中阴影部分的面积为．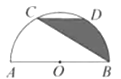

查看试题解析
14. 已知抛物线y=ax²﹣2ax+c与x轴一个交点的坐标为（﹣1，0），则一元二次方程ax²﹣2ax+c=0的根为．

查看试题解析
15. 如图，矩形ABCD中，AB=1，AD=2，点E是边AD上的一个动点，把△BAE沿BE折叠，点A落在A′处，如果A′恰在矩形的对称轴上，则AE的长为．

查看试题解析

三、解答题

16. 已知：关于x的方程x²+2mx+m²-1=0

(1)、不解方程，判别方程根的情况；

(2)、若方程有一个根为3，求m的值．

查看试题解析
17. 一个不透明的布袋里装有2个白球，1个黑球和若干个红球，它们除颜色外其余都相同．从中任意摸出1个球，取出白球的概率为 $\frac{1}{2}$ ．

(1)、布袋里红球有个；

(2)、先从布袋中摸出1个球后不再放回，再摸出1个球，求两次摸到的球都是白球的概率．

查看试题解析
18. 某校七年级共有500名学生，团委准备调查他们对“低碳”知识的了解程度，

(1)、在确定调查方式时，团委设计了以下三种方案：
方案一：调查七年级部分女生；
方案二：调查七年级部分男生；
方案三：到七年级每个班去随机调查一定数量的学生
请问其中最具有代表性的一个方案是

(2)、团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将其补充完整；

(3)、请你估计该校七年级约有多少名学生比较了解“低碳”知识．

查看试题解析
19. 如图，已知抛物线y= $- x^{2}$ +mx+3与x轴交于A，B两点，与y轴交于点C，点B的坐标为（3，0），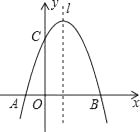

(1)、求m的值及抛物线的顶点坐标．

(2)、点P是抛物线对称轴l上的一个动点，当PA+PC的值最小时，求点P的坐标．

查看试题解析
20. 如图，某校八年级（1）班学生利用寒假期间到郊区进行社会实践活动，活动之余，同学们准备攀登附近的一个小山坡，从B点出发，沿坡脚15°的坡面以5千米/时的速度行至D点，用了10分钟，然后沿坡比为1： $\sqrt{3}$ 的坡面以3千米/时的速度达到山顶A点，用了5分钟，求小山坡的高（即AC的长度）（精确到0.01千米）（sin15°≈0.2588，cos15°≈0.9659， $\sqrt{3}$ ≈1.732）

查看试题解析
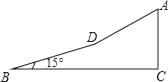21. 如图，已知AB为⊙O的直径，BD和CD为⊙O的切线，切点分别为B和C．

(1)、求证：AC∥OD；

(2)、当BC=BD，且BD=6cm时，求图中阴影部分的面积（结果不取近似值）．

查看试题解析
22.

(1)、问题发现
如图1，四边形ABCD为矩形，AB=a，BC=b，点P在矩形ABCD的对角线AC上，Rt△PEF的两条直角边PE，PF分别交BC，DC于点M，N，当PM⊥BC，PN⊥CD时， $\frac{P M}{P N}$ =（用含a，b的代数式表示）．

(2)、拓展探究
在（1）中，固定点P，使△PEF绕点P旋转，如图2， $\frac{P M}{P N}$ 的大小有无变化？请仅就图2的情形给出证明．

(3)、问题解决
如图3，四边形ABCD为正方形，AB=BC=a，点P在对角线AC上，M，N分别在BC，CD上，PM⊥PN，当AP=nPC时，（n是正实数），直接写出四边形PMCN的面积是（用含n，a的代数式表示）

查看试题解析
23. 如图，直线y=x+2与抛物线y=ax²+bx+6相交于A（ $\frac{1}{2}$ ， $\frac{5}{2}$ ）和B（4，m），点P是AB上的动点，设点P的横坐标为n，过点P作PC⊥x轴，交抛物线于点C，与x轴交于M点．

(1)、求抛物线的表达式；

(2)、点P是线段AB上异于A，B的动点，是否存在这样的点P，使线段PC的长有最大值？若存在，求出这最大值，若不存在，请说明理由；

(3)、点P在直线AB上自由移动，当三个点C，P，M中恰有一点是其它两点所连线段的中点时，请直接写出m的值．

查看试题解析

日期	1日	2日	3日	4日	5日	6日	7日	8日
电表显示度数(度)	115	118	122	127	133	136	140	143

x	…	﹣2	﹣1	0	1	2	…
y	…	0	4	6	6	4	…