2016-2017学年浙江省台州市玉环县十校九年级上学期期中数学试卷
试卷更新日期:2017-02-16 类型:期中考试
一、选择题
-
1. 二次函数y=x2﹣8x+15的图象与x轴相交于M,N两点,点P在该函数的图象上运动,能使△PMN的面积等于的点P共有( )
A、1个 B、2个 C、3个 D、4个2. 二次函数y=a(x﹣4)2﹣4(a≠0)的图象在2<x<3这一段位于x轴的下方,在6<x<7这一段位于x轴的上方,则a的值为( )A、1 B、﹣1 C、2 D、﹣23. 如图,已知函数y=ax2+bx+c(a≠0),有下列四个结论:①abc>0;②4a+2b+c>0;③3a+c<0;④a+b≥m(am+b),其中正确的有( )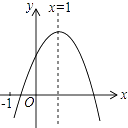 A、1个 B、2个 C、3个 D、4个4. 下列说法正确的是( )A、任意三点可以确定一个圆 B、平分弦的直径垂直于弦,并且平分该弦所对的弧 C、同一平面内,点P到⊙O上一点的最小距离为2,最大距离为8,则该圆的半径为5 D、同一平面内,点P到圆心O的距离为5,且圆的半径为10,则过点P且长度为整数的弦共有5条5. 将量角器按如图摆放在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )
A、1个 B、2个 C、3个 D、4个4. 下列说法正确的是( )A、任意三点可以确定一个圆 B、平分弦的直径垂直于弦,并且平分该弦所对的弧 C、同一平面内,点P到⊙O上一点的最小距离为2,最大距离为8,则该圆的半径为5 D、同一平面内,点P到圆心O的距离为5,且圆的半径为10,则过点P且长度为整数的弦共有5条5. 将量角器按如图摆放在三角形纸板上,使点C在半圆上.点A、B的读数分别为86°、30°,则∠ACB的大小为( )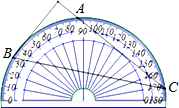 A、15° B、28° C、30° D、56°6. 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上任意一点,连结AD,GD. =50°,则∠AGD=( )
A、15° B、28° C、30° D、56°6. 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是 上任意一点,连结AD,GD. =50°,则∠AGD=( )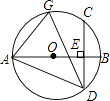 A、50° B、55° C、65° D、75°7. 如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )
A、50° B、55° C、65° D、75°7. 如图,AC,BD为圆O的两条互相垂直的直径,动点P从圆心O出发,沿O→C→D→O的路线作匀速运动,设运动时间为t秒,∠APB的度数为y度,那么表示y与t之间函数关系的图象大致为( )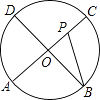 A、
A、 B、
B、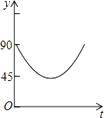 C、
C、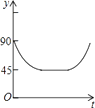 D、
D、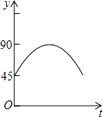 8. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为( )
8. 如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB=30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为7,则GE+FH的最大值为( )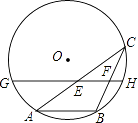 A、10.5 B、7 ﹣3.5 C、11.5 D、7 ﹣3.59. 已知二次函数y=x2﹣bx+1(﹣1≤b≤1),当b从﹣1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )A、先往左上方移动,再往左下方移动 B、先往左下方移动,再往左上方移动 C、先往右上方移动,再往右下方移动 D、先往右下方移动,再往右上方移动10. 已知两点A(﹣5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0 , y0)是该抛物线的顶点.若y1>y2≥y0 , 则x0的取值范围是( )A、x0>﹣5 B、x0>﹣1 C、﹣5<x0<﹣1 D、﹣2<x0<3
A、10.5 B、7 ﹣3.5 C、11.5 D、7 ﹣3.59. 已知二次函数y=x2﹣bx+1(﹣1≤b≤1),当b从﹣1逐渐变化到1的过程中,它所对应的抛物线位置也随之变动.下列关于抛物线的移动方向的描述中,正确的是( )A、先往左上方移动,再往左下方移动 B、先往左下方移动,再往左上方移动 C、先往右上方移动,再往右下方移动 D、先往右下方移动,再往右上方移动10. 已知两点A(﹣5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0 , y0)是该抛物线的顶点.若y1>y2≥y0 , 则x0的取值范围是( )A、x0>﹣5 B、x0>﹣1 C、﹣5<x0<﹣1 D、﹣2<x0<3二、选择题
-
11. 如图在平面直角坐标系中,过格点A,B,C作一圆弧,圆心坐标是 .
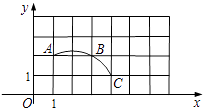 12. 如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 .
12. 如图,在半径为5的⊙O中,AB、CD是互相垂直的两条弦,垂足为P,且AB=CD=8,则OP的长为 .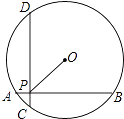 13. 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2﹣2x,其对称轴与两抛物线所围成的阴影部分的面积是 .
13. 如图,在平面直角坐标系中,抛物线y=x2经过平移得到抛物线y=x2﹣2x,其对称轴与两抛物线所围成的阴影部分的面积是 .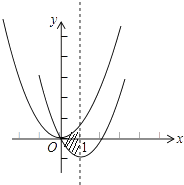 14. 若抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于正半轴C点,且AC=20,BC=15,∠ACB=90°,则此抛物线的解析式为 .15. 在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .16. 二次函数 的图象如图所示,点A0位于坐标原点,点A1 , A2 , A3 , …,A2008在y轴的正半轴上,点B1 , B2 , B3 , …,B2008在二次函数 位于第一象限的图象上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长= .
14. 若抛物线y=ax2+bx+c与x轴交于A,B两点,与y轴交于正半轴C点,且AC=20,BC=15,∠ACB=90°,则此抛物线的解析式为 .15. 在Rt△ABC中,∠C=90°,BC=3,AC=4,点P在以C为圆心,5为半径的圆上,连结PA,PB.若PB=4,则PA的长为 .16. 二次函数 的图象如图所示,点A0位于坐标原点,点A1 , A2 , A3 , …,A2008在y轴的正半轴上,点B1 , B2 , B3 , …,B2008在二次函数 位于第一象限的图象上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都为等边三角形,则△A2007B2008A2008的边长= .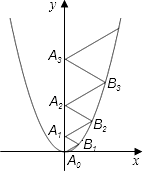
三、解答题
-
17. 课堂上,师生一起探究知,可以用已知半径的球去测量圆柱形管子的内径.小明回家后把半径为5cm的小皮球置于保温杯口上,经过思考找到了测量方法,并画出了草图(如图).请你根据图中的数据,帮助小明计算出保温杯的内径.
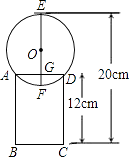 18. 如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.
18. 如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE,求证:BD=DE.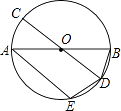 19. 解答题(1)、作△ABC的外接圆;(2)、若AC=BC,AB=8,C到AB的距离是2,求△ABC的外接圆半径.
19. 解答题(1)、作△ABC的外接圆;(2)、若AC=BC,AB=8,C到AB的距离是2,求△ABC的外接圆半径.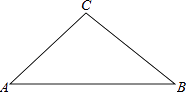 20. 如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.
20. 如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.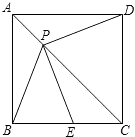 (1)、求证:①PE=PD;②PE⊥PD;(2)、设AP=x,△PBE的面积为y.
(1)、求证:①PE=PD;②PE⊥PD;(2)、设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;
②当x取何值时,y取得最大值,并求出这个最大值.
21. 九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:时间x(天)
1≤x<50
50≤x≤90
售价(元/件)
x+40
90
每天销量(件)
200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)、求出y与x的函数关系式;(2)、问销售该商品第几天时,当天销售利润最大,最大利润是多少?(3)、该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.22. 如图,抛物线 与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).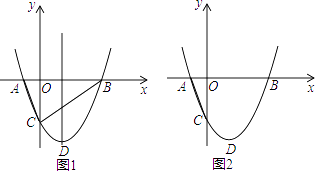 (1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M是抛物线对称轴上的一个动点,当CM+AM的值最小时,求M的坐标;(4)、在线段BC下方的抛物线上有一动点P,求△PBC面积的最大值.
(1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M是抛物线对称轴上的一个动点,当CM+AM的值最小时,求M的坐标;(4)、在线段BC下方的抛物线上有一动点P,求△PBC面积的最大值.