人教A版高中数学必修二 2.1.1平面 同步练习
试卷更新日期：2018-08-01 类型：同步测试
一、单选题
-
1. 下列叙述正确的是（ ）A、若P∈α，Q∈α，则PQ∈α B、若P∈α，Q∈β，则α∩β=PQ C、若AB⊂α，C∈AB，D∈AB，则CD∈α D、若AB⊂α，AB⊂β，则A∈α∩β且B∈α∩β2. 下面说法中(其中A，B表示点，a表示直线，α表示平面)：
①因为A⊂α，B⊂α，所以AB⊂α；
②因为A∈α，B∈α，所以AB∈α；
③因为A∉a，a⊂α，所以A∉α；
④因为A∉α，a⊂α，所以A∉a.
其中正确的说法的序号是（ ）
A、①④ B、②③ C、④ D、③3. 下列说法中正确的个数为（ ）①三角形一定是平面图形；
②若四边形的两对角线相交于一点，则该四边形是平面图形；
③圆心和圆上两点可确定一个平面；
④三条平行线最多可确定三个平面.
A、1 B、2 C、3 D、44. 已知A，B是点，a，b，l是直线，α是平面，如果a⊂α，b⊂α，l∩a=A，l∩b=B，那么下列关系中成立的是（ ）A、l⊂α B、l∈α C、l∩α=A D、l∩α=B5. 用符号语言表示下列语句，正确的个数是（ ）⑴点A在平面α内，但不在平面β内：A⊂α，A⊄β.
⑵直线a经过平面α外的点A，且a不在平面α内：A∈a，A∉α，a⊄α.
⑶平面α与平面β相交于直线l ， 且l经过点P：α∩β=l ， P∈l.
⑷直线l经过平面α外一点P，且与平面α相交于点M：P∈l ， l∩α=M.
A、1 B、2 C、3 D、46. 一条直线和直线外三个点最多能确定的平面个数是（ ）A、4 B、6 C、7 D、107. 如图所示，平面α∩β＝l ， A、B∈α ， C∈β且C∉l ， AB∩l＝R ， 设过A、B、C三点的平面为γ ， 则β∩γ等于 （ ）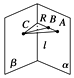
A、直线AC B、直线BC C、直线CR D、以上都不对8. 在空间四边形ABCD的边AB，BC，CD，DA上分别取E，F，G，H四点，如EF与HG交于点M，那么（ ）A、M一定在直线AC上 B、M一定在直线BD上 C、M可能在直线AC上，也可能在直线BD上 D、M既不在直线AC上，也不在直线BD上二、填空题
-
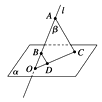
9. AB，AD⊂α，CB，CD⊂β，E∈AB，F∈BC，G∈CD，H∈DA，若直线EH与FG相交于点P，则点P必在直线上.10. 若直线l与平面α相交于点O、A、B∈l、C、D∈α ， 且AC∥∥BD ， 则O、C、D三点的位置关系是.
三、解答题
