2016-2017学年山东省济宁市邹城八中九年级上学期期中数学试卷
试卷更新日期:2017-02-16 类型:期中考试
一、选择题
-
1. 如图,所给图形中是中心对称图形但不是轴对称图形的是( )A、
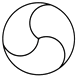 B、
B、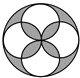 C、
C、 D、
D、 2. 对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个交点3. 如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
2. 对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个交点3. 如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )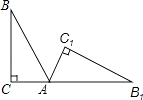 A、115° B、120° C、125° D、145°4. 若二次函数y=x2+bx的图象的对称轴是直线x=2,则关于x的方程x2+bx=﹣4的解为( )A、x1=0,x2=4 B、x1=x2=2 C、x1=2,x2=﹣2 D、x1=x2=﹣25. 关于x的方程x2+2kx﹣1=0的根的情况描述正确的是( )A、k为任何实数,方程都没有实数根 B、k为任何实数,方程都有两个不相等的实数根 C、k为任何实数,方程都有两个相等的实数根 D、k取值不同实数,方程实数根的情况有三种可能6. 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为( )
A、115° B、120° C、125° D、145°4. 若二次函数y=x2+bx的图象的对称轴是直线x=2,则关于x的方程x2+bx=﹣4的解为( )A、x1=0,x2=4 B、x1=x2=2 C、x1=2,x2=﹣2 D、x1=x2=﹣25. 关于x的方程x2+2kx﹣1=0的根的情况描述正确的是( )A、k为任何实数,方程都没有实数根 B、k为任何实数,方程都有两个不相等的实数根 C、k为任何实数,方程都有两个相等的实数根 D、k取值不同实数,方程实数根的情况有三种可能6. 如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内 上一点,∠BMO=120°,则⊙C的半径长为( ) A、6 B、5 C、3 D、37. 如图,抛物线y=ax2+bx+c与x轴交于点(﹣1,0),对称轴为x=1,则下列结论中正确的是( )
A、6 B、5 C、3 D、37. 如图,抛物线y=ax2+bx+c与x轴交于点(﹣1,0),对称轴为x=1,则下列结论中正确的是( ) A、a>0 B、当x>1时,y随x的增大而增大 C、c<0 D、x=3是一元二次方程ax2+bx+c=0的一个根8. 如图,在△ABC中,∠B=90°,AB=4,BC=3,将△ABC绕点A逆时针旋转,使点B落在线段AC上的点D处,点C落在点E处,则C、E两点间的距离为( )
A、a>0 B、当x>1时,y随x的增大而增大 C、c<0 D、x=3是一元二次方程ax2+bx+c=0的一个根8. 如图,在△ABC中,∠B=90°,AB=4,BC=3,将△ABC绕点A逆时针旋转,使点B落在线段AC上的点D处,点C落在点E处,则C、E两点间的距离为( ) A、 B、2 C、3 D、29. 如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( )
A、 B、2 C、3 D、29. 如图,Rt△ABC的斜边AB与量角器的直径恰好重合,B点与0刻度线的一端重合,∠ABC=40°,射线CD绕点C转动,与量角器外沿交于点D,若射线CD将△ABC分割出以BC为边的等腰三角形,则点D在量角器上对应的度数是( ) A、40° B、70° C、70°或80° D、80°或140°10. 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( )
A、40° B、70° C、70°或80° D、80°或140°10. 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P、Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 一元二次方程x(x﹣2)=2﹣x的正整数根是 .12. 如图,在一个正方形围栏中均匀散布着许多米粒,正方形内画有一个圆.一只小鸡在围栏内啄食,则“小鸡正在圆圈内”啄食的概率为 .
 13. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为 .
13. 如图,AB为⊙O的直径,直线l与⊙O相切于点C,AD⊥l,垂足为D,AD交⊙O于点E,连接OC、BE.若AE=6,OA=5,则线段DC的长为 . 14. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为 .
14. 如图,正六边形ABCDEF内接于半径为3的圆O,则劣弧AB的长度为 .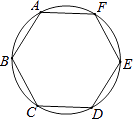 15.
15.如图,在平面直角坐标系中,点A,B,C的坐标分别为(1,0),(0,1),(﹣1,0).一个电动玩具从坐标原点0出发,第一次跳跃到点P1 . 使得点P1与点O关于点A成中心对称;第二次跳跃到点P2 , 使得点P2与点P1关于点B成中心对称;第三次跳跃到点P3 , 使得点P3与点P2关于点C成中心对称;第四次跳跃到点P4 , 使得点P4与点P3关于点A成中心对称;第五次跳跃到点P5 , 使得点P5与点P4关于点B成中心对称;…照此规律重复下去,则点P7的坐标是 , 点P2016的坐标为

三、解答题
-
16. 已知:平行四边形ABCD的两边AB、AD的长是关于x的方程x2﹣mx+ =0的两个实数根.(1)、m为何值时,四边形ABCD是菱形?求出这时菱形的边长;(2)、若AB的长为2,那么平行四边形ABCD的周长是多少?17. 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A,B,C都在格点上,将△ABC绕点A按顺时针方向旋转90°得到△AB′C′.
 (1)、在正方形网格中,画出△AB′C′;(2)、计算线段AB在变换到AB′的过程中扫过区域的面积.18. 小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.(1)、用列表法或画树状图法,求小丽参赛的概率.(2)、你认为这个游戏公平吗?请说明理由.19. 如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°.
(1)、在正方形网格中,画出△AB′C′;(2)、计算线段AB在变换到AB′的过程中扫过区域的面积.18. 小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.(1)、用列表法或画树状图法,求小丽参赛的概率.(2)、你认为这个游戏公平吗?请说明理由.19. 如图,AB为⊙O的直径,AC、DC为弦,∠ACD=60°,P为AB延长线上的点,∠APD=30°. (1)、求证:DP是⊙O的切线;(2)、若⊙O的半径为3cm,求图中阴影部分的面积.20. 某食品零售店为仪器厂代销一种面包,未售出的面包可退回厂家,以统计销售情况发现,当这种面包的单价定为7角时,每天卖出160个.在此基础上,这种面包的单价每提高1角时,该零售店每天就会少卖出20个.考虑了所有因素后该零售店每个面包的成本是5角.
(1)、求证:DP是⊙O的切线;(2)、若⊙O的半径为3cm,求图中阴影部分的面积.20. 某食品零售店为仪器厂代销一种面包,未售出的面包可退回厂家,以统计销售情况发现,当这种面包的单价定为7角时,每天卖出160个.在此基础上,这种面包的单价每提高1角时,该零售店每天就会少卖出20个.考虑了所有因素后该零售店每个面包的成本是5角.设这种面包的单价为x(角),零售店每天销售这种面包所获得的利润为y(角).
(1)、用含x的代数式分别表示出每个面包的利润与卖出的面包个数;(2)、求y与x之间的函数关系式;(3)、当面包单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少?21. 小明是个爱动脑筋的孩子,他在学完与圆有关的角圆周角、圆心角后,意犹未尽,又查阅到了与圆有关的另一种角﹣﹣﹣﹣﹣﹣弦切角.请同学们先仔细阅读下面的材料,再完成后面的问题.材料:顶点在圆上,一边与圆相交,另一边与圆相切的角叫做弦切角.如图1,弧 是弦切角∠PAB所夹的弧,他发现弦切角与它所夹的弧所对的圆周角有关系.

问题1:如图2,直线DB切⊙O于点A,∠PCA是圆周角,当圆心O位于边AC上时,
求证:∠PAD=∠PCA,请你写出这个证明过程.
问题拓展:
如果圆心O不在∠PCA的边上,∠PAD=∠PCA还成立吗?如图3,当圆心O在∠PCA的内部时,小明证明了这个结论是成立的.他的思路是:作直线AE,联结PE,由问题1的结论可知∠PAD=∠PEA,而∠PCA=∠PEA,从而证明∠PAD=∠PC.
问题2:如图4,当圆心O在∠PCA的外部时,∠PAD=∠PCA仍然成立.请你仿照小明的思路证明这个结论.
运用:如图5,AD是△ABC中∠BAC的平分线,经过点A的⊙O与BC切于点D,与AB、AC分别相交于E、F.求证:EF∥BC.(提示:可以直接使用本题中的结论)
22. 如图,抛物线y=x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3). (1)、求抛物线的解析式;(2)、若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;(3)、在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、若点M是抛物线在x轴下方上的动点,过点M作MN∥y轴交直线BC于点N,求线段MN的最大值;(3)、在(2)的条件下,当MN取得最大值时,在抛物线的对称轴l上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.