2016-2017学年辽宁省抚顺市新宾县九年级上学期期中数学试卷
试卷更新日期:2017-02-16 类型:期中考试
一、选择题
-
1. 下列方程是关于x的一元二次方程的是( )A、ax2+bx+c=0 B、 +4x=6 C、x2﹣3x=x2﹣2 D、(x+1)(x﹣1)=2x2. 下列汽车标志可以看作是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是( )A、(3,﹣2) B、(2,3) C、(﹣2,﹣3) D、(2,﹣3)4. 若某商品的原价为100元,连续两次涨价后的售价为144元,设两次平增长率为x.则下面所列方程正确的是( )A、100(1﹣x)2=144 B、100(1+x)2=144 C、100(1﹣2x)2=144 D、100(1+2x)2=1445. 对抛物线:y=﹣x2+2x﹣3而言,下列结论正确的是( )A、与x轴有两个交点 B、开口向上 C、与y轴的交点坐标是(0,3) D、顶点坐标是(1,﹣2)6. 若将函数y=2x2的图象向左平移1个单位,再向上平移3个单位,可得到的抛物线是( )A、y=2(x﹣1)2﹣3 B、y=2(x﹣1)2+3 C、y=2(x+1)2﹣3 D、y=2(x+1)2+37. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、
3. 平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是( )A、(3,﹣2) B、(2,3) C、(﹣2,﹣3) D、(2,﹣3)4. 若某商品的原价为100元,连续两次涨价后的售价为144元,设两次平增长率为x.则下面所列方程正确的是( )A、100(1﹣x)2=144 B、100(1+x)2=144 C、100(1﹣2x)2=144 D、100(1+2x)2=1445. 对抛物线:y=﹣x2+2x﹣3而言,下列结论正确的是( )A、与x轴有两个交点 B、开口向上 C、与y轴的交点坐标是(0,3) D、顶点坐标是(1,﹣2)6. 若将函数y=2x2的图象向左平移1个单位,再向上平移3个单位,可得到的抛物线是( )A、y=2(x﹣1)2﹣3 B、y=2(x﹣1)2+3 C、y=2(x+1)2﹣3 D、y=2(x+1)2+37. 若关于x的一元二次方程x2﹣2x+kb+1=0有两个不相等的实数根,则一次函数y=kx+b的大致图象可能是( )A、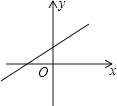 B、
B、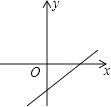 C、
C、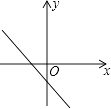 D、
D、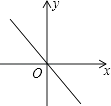 8. 若5k+20<0,则关于x的一元二次方程x2+4x﹣k=0的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断9. 已知二次函数y=kx2﹣2x﹣1的图象和x轴有交点,则k的取值范围是( )A、k>﹣1 B、k<1 C、k≥﹣l且k≠0 D、k<1且k≠010. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a﹣b+c>0; ④4a+2b+c<0.其中错误的结论有( )
8. 若5k+20<0,则关于x的一元二次方程x2+4x﹣k=0的根的情况是( )A、没有实数根 B、有两个相等的实数根 C、有两个不相等的实数根 D、无法判断9. 已知二次函数y=kx2﹣2x﹣1的图象和x轴有交点,则k的取值范围是( )A、k>﹣1 B、k<1 C、k≥﹣l且k≠0 D、k<1且k≠010. 如图是二次函数y=ax2+bx+c图象的一部分,且过点A (3,0),二次函数图象的对称轴是x=1.下列结论:①b2>4ac;②ac>0; ③a﹣b+c>0; ④4a+2b+c<0.其中错误的结论有( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. 二次函数y=﹣(x+1)2+8的开口方向是 .12. 已知x1 , x2是方程x2+2x﹣k=0的两个实数根,则x1+x2= .13. 小明用30厘米的铁丝围成一斜边等于13厘米的直角三角形,设该直角三角形一直角边长x厘米,根据题意列方程为14. 如图,在平面直角坐标系中,将线段AB绕点A按逆时针方向旋转90°后,得到线段AB′,则点B′的坐标为 .
 15. 已知一元二次方程(a+3)x2+4ax+a2﹣9=0有一个根为0,则a= .16. 如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角的度数是
15. 已知一元二次方程(a+3)x2+4ax+a2﹣9=0有一个根为0,则a= .16. 如图,将Rt△ABC(其中∠B=35°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角的度数是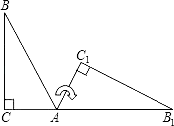 17. 抛物线y=2x2﹣bx+3的对称轴是直线x=1,则该函数的最小值是18. 图1是棱长为a的小正方体,图2、图3出这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…,第n层,第n层的小正方体的个数为s.(提示:第一层时,s=1;第二层时,s=3)则第n层时,s=(用含n的式子表示)
17. 抛物线y=2x2﹣bx+3的对称轴是直线x=1,则该函数的最小值是18. 图1是棱长为a的小正方体,图2、图3出这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…,第n层,第n层的小正方体的个数为s.(提示:第一层时,s=1;第二层时,s=3)则第n层时,s=(用含n的式子表示)
三、解答题
-
19. 解方程:(1)、x2+4x+2=0(配方法)(2)、5x2+5x=﹣1﹣x(公式法)20. 如图所示,方格纸中的每个小方格都是边长为1个单位长度的正方形,建立平面直角坐标系,△ABC的顶点均在格点上.(不写作法)
①以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1 , 并写出B1的坐标;
②再把△A1B1C1绕点C1 , 顺时针旋转90°,得到△A2B2C2 , 请你画出△A2B2C2 , 并写出B2的坐标.
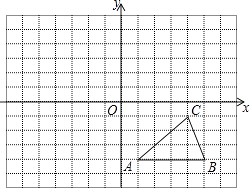 21. 关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2 .(1)、求k的取值范围;(2)、如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.22. 如图,直线y=﹣ x+1和抛物线y=x2+bx+c都经过点A(2,0)和点B(k, )
21. 关于x的一元二次方程x2+2x+k+1=0的实数解是x1和x2 .(1)、求k的取值范围;(2)、如果x1+x2﹣x1x2<﹣1且k为整数,求k的值.22. 如图,直线y=﹣ x+1和抛物线y=x2+bx+c都经过点A(2,0)和点B(k, ) (1)、k的值是;(2)、求抛物线的解析式;(3)、不等式x2+bx+c>﹣ x+1的解集是 .23. 有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米.
(1)、k的值是;(2)、求抛物线的解析式;(3)、不等式x2+bx+c>﹣ x+1的解集是 .23. 有一座抛物线形拱桥,校下面在正常水位时AB宽20米,水位上升3米就达到警戒线CD,这时水面宽度为10米. (1)、在如图的坐标系中,求抛物线的表达式;(2)、若洪水到来是水位以0.2米/时的速度上升,从正常水位开始,再过几小时能到达桥面?24. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件;(1)、若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场平均每天赢利最多?25. 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)、在如图的坐标系中,求抛物线的表达式;(2)、若洪水到来是水位以0.2米/时的速度上升,从正常水位开始,再过几小时能到达桥面?24. 某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件;(1)、若商场平均每天要赢利1200元,每件衬衫应降价多少元?(2)、每件衬衫降价多少元时,商场平均每天赢利最多?25. 如图所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动. (1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?(2)、是否存在某一时刻,使△PCQ的面积等于△ABC面积的一半,并说明理由.(3)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积达到最大值,并说明利理由.26. 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?(2)、是否存在某一时刻,使△PCQ的面积等于△ABC面积的一半,并说明理由.(3)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积达到最大值,并说明利理由.26. 已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB. (1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(1)、求抛物线的解析式;(2)、若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.