2015-2016学年江苏省淮安市淮安区八年级下学期期中数学试卷
试卷更新日期：2017-02-15 类型：期中考试
一、选择题
-
1.
下列四张扑克牌中，属于中心对称的图形是（ ）
A、红桃7 B、方块4 C、梅花6 D、黑桃52. 下列样本的选取具有代表性的是（ ）A、利用某地七月份的日平均气温估计当地全年的日平均气温 B、为了解我国居民的年平均阅读时间，从大学生中随机抽取10万人进行抽查 C、调查某些七年级（1）班学生的身高；来估计该校全体学生的身高 D、为了了解一批洗衣粉的质量情况，从仓库中任意抽取100袋进行检验3. 从只装有4个红球的袋中随机摸出一球，若摸到白球的概率是p1 ， 摸到红球的概率是p2 ， 则（ ）A、p1=1，p2=1 B、p1=0，p2=1 C、p1=0，p2= D、p1=p2=4. 已知▱ABCD中，若∠A+∠C=120°，则∠B的度数是（ ）A、100° B、120° C、80° D、60°5. 某校图书管理员清理课外书籍时，将其中甲、乙、丙三类书籍的有关数据制成如图不完整的统计图，已知甲类书有30本，则丙类书的本数是（ ）
A、80 B、144 C、200 D、906. 如图，E是正方形ABCD的边BC延长线上一点，且CE=AC，则∠E=（ ）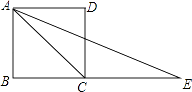
A、90° B、45° C、30° D、22.5°7. 菱形具有而矩形不一定具有的性质是（ ）A、内角和等于360° B、对角相等 C、对角线互相垂直 D、对边平行且相等8. 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）
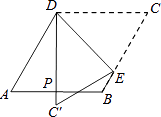A、78° B、75° C、60° D、45°二、填空题
-
9. 在菱形ABCD中，AB=5，则BC= ．10. 平行四边形的周长为24cm，相邻两边长的比为3：1，那么这个平行四边形较短的边长为 cm．11. 袋中共有2个红球，4个黄球，从中任取一个球是白球，这个事件是事件．12. 袋子里有5只红球，3只白球，每只球除颜色以外都相同，从中任意摸出1只球，是红球的可能性（选填“大于”“小于”或“等于”）是白球的可能性．13. 若四边形的两条对角线垂直，则顺次连接该四边形各边中点所得的四边形是 ．14. 某校公布了反映该校各年级学生体育达标情况的两张统计图，该校七、八、九三个年级共有学生800人．甲、乙、丙三个同学看了这两张图后，甲说：“七年级的体育达标率最高．”乙说：“八年级共有学生264人．”丙说：“九年级的体育达标率最高．”甲、乙、丙三个同学中，说法错误的是 ．
15. 在四边形ABCD中，AB=DC，AD=BC，请再添加一个条件，使四边形ABCD是矩形．你添加的条件是 ． （写出一种即可）16. 如图，在正方形ABCD的外侧，作等边△ADE，则∠BED的度数是 ．
17. 如图，在▱ABCD中，AD=6，点E、F分别是BD、CD的中点，则EF=
18. 如图，在长方形ABCD中，E是AD的中点，F是CE的中点．若△BDF的面积是5平方厘米，则长方形ABCD的面积是平方厘米．
三、解答题
-
19. 如图，四边形ABCD中，AB∥CD，∠B=∠D，BC=6，AB=3，求四边形ABCD的周长．
20. 如图，作出将△ABC绕点O逆时针旋转180°后的△A1B1C1 ．
21. 如图，已知：AB∥CD，BE⊥AD，垂足为点E，CF⊥AD，垂足为点F，并且AE=DF．
求证：
(1)、BE=CF；(2)、四边形BECF是平行四边形．22. 某校想了解学生每周的课外阅读时间情况，随机调查了部分学生，对学生每周的课外阅读时间x（单位：小时）进行分组整理，并绘制了如图所示的不完整的频数分布直方图和扇形统计图：
根据图中提供的信息，解答下列问题：
(1)、共随机调查了名学生，课外阅读时间在6﹣8小时之间有人，并补全频数分布直方图(2)、求扇形统计图中m的值和E组对应的圆心角度数；(3)、请估计该校3000名学生每周的课外阅读时间不小于6小时的人数．23. 一只不透明的袋子中有2个红球、3个绿球和5个白球，这些球处颜色外都相同，将球搅匀，从中任意摸出1个球．(1)、会出现哪些可能的结果？(2)、能够确定摸到的一定是红球吗？(3)、你认为摸到哪种颜色的球可能性最大？哪种颜色的球可能性最小？(4)、怎样改变袋子中红球、绿球和白球的个数，使摸到这三种颜色的球的概率相同？24. 如图，矩形ABCD中，AC与BD交于O点，BE⊥AC于E，CF⊥BD于F．
求证：
(1)、∠ACB=∠DBC；(2)、BE=CF．25. 在▱ABCD中，点O是对角线AC、BD的交点，AC垂直于BC，且AB=10cm，AD=8cm．
求：
(1)、AC的长；(2)、求OB的长．26. 已知：如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．
(1)、求证：△ABM≌△DCM；(2)、判断四边形MENF是什么特殊四边形，并证明你的结论；(3)、当AD：AB=时，四边形MENF是正方形（只写结论，不需证明）．27. 如图①，已知△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点．作正方形DEFG，使点A，C分别在DG、DE上，连接AE、BG．
(1)、试猜想线段BG和AE的数量关系，请直接写出你得到的结论；(2)、将正方形DEFG绕点D逆时针方向旋转一定角度后（旋转角度大于0°，小于或等于360°），如图②，（1）中的结论是否仍然成立？如果成立，请予以证明；如果不成立，请说明理由．