2015-2016学年湖南省邵阳市武冈市八年级下学期期中数学试卷
试卷更新日期：2017-02-15 类型：期中考试
一、选择题
-
1. 下列图形中，是中心对称图形的是（ ）A、
B、
C、
D、
2. 下列条件中，能判定四边形为平行四边形的是（ ）A、对角线相互垂直 B、对角线互相平分 C、一组对角相等 D、一组对边相等3. 下列几组数中，能作为直角三角形三边长度的是（ ）A、3，5，6 B、1，1， C、5，8，11 D、5，12，154.如图，四边形ABCD的对角线互相平分，要使它成为矩形，那么需要添加的条件是（ ）
A、AB=CD B、AD=BC C、AB=BC D、AC=BD5. 一个多边形的内角和是外角和的2倍，则这个多边形的边数为（ ）A、4 B、5 C、6 D、76. 如图，在▱ABCD中，∠ODA=90°，AC=10cm，BD=6cm，则BC的长为（ ）
A、4cm B、5cm C、6cm D、8cm7. 若△ABC的两边长为4和5，则能使△ABC是直角三角形的第三边的平方是（ ）A、9 B、41 C、3 D、9或418. 顺次连接矩形四边中点所得的四边形一定是（ ）A、正方形 B、矩形 C、菱形 D、等腰梯形9. 如图，已知矩形ABCD中，R，P分别是DC、BC上的点，E，F分别是AP，RP的中点，当P在BC上从B向C移动而R不动时，那么下列结论成立的是（ ）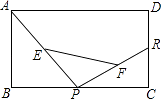
A、线段EF的长逐渐增大 B、线段EF的长逐渐减小 C、线段EF的长不改变 D、线段EF的长不能确定10. 如图，矩形纸片ABCD中，AB=4，AD=3，折叠纸片使AD边与对角线BD重合，折痕为DG，则AG的长为（ ）
A、1 B、 C、 D、2二、填空题
-
11. 一个多边形的每一个外角都等于36°，它是边形．12. △ABC的周长为16，点D，E，F分别是△ABC的边AB、BC、CA的中点，连接DE，EF，DF，则△DEF的周长是 ．13. 已知菱形的两条对角线长为6cm和8cm，菱形的周长是 cm，面积是 cm2 ．14. 一棵树因雪灾于A处折断，如图所示，测得树梢触地点B到树根C处的距离为4米，∠ABC约45°，树干AC垂直于地面，那么此树在未折断之前的高度约为米（答案可保留根号）
15. 平行四边形的周长等于56cm，两邻边长的比为3：1，那么这个平行四边形较长的边长为 cm．16. 如图在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于D，如果AE+DE=3cm，那么AC= ．
17. 如图是一个三级台阶，它的每一级的长、宽和高分别为25dm、3dm、3dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到 B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是 ． （结果保留根号）
18. 如图，依次连结第一个矩形各边的中点得到一个菱形，再依次连结菱形各边的中点得到第二个矩形，按照此方法继续下去．已知第一个矩形的面积为s，则第n个矩形的面积为 ．
三、解答题
-
19. 若a、b、c为△ABC三边长，且a、b、c满足（a﹣5）2+（b﹣12）2+|c﹣13|=0，△ABC是直角三角形吗？请说明理由．20. 如图，在▱ABCD中，点E，F分别在BC，AD上，且DF=BE．
求证：四边形AECF是平行四边形．
21. 如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．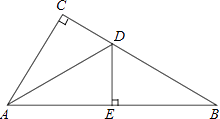
(1)、求证：△ACD≌△AED；(2)、若∠B=30°，CD=1，求BD的长．22. 已知：如图所示，矩形ABCD中，E是BC上的一点，且AE=BC，∠EDC=15°．求证：AD=2AB．
23. 已知：如图，为了躲避台风，一轮船一直由西向东航行，上午10点，在A处测得小岛P的方向是北偏东75°，以每小时15海里的速度继续向东航行，中午12点到达B处，并测得小岛P的方向是北偏东60°，若小岛周围25海里内有暗礁，问该轮船是否能一直向东航行？
