2015-2016学年湖北省宜昌五中八年级下学期期中数学试卷

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下列各组数分别为一个三角形三边的长，其中能构成直角三角形的一组是（）

A、1，2，3 B、2，3，4 C、3，4，5 D、4，5，6

查看试题解析
2. 图中的四边形均为正方形，三角形为直角三角形，最大的正方形的边长为7cm，则图中A，B两个正方形的面积之和为（）

A、28cm² B、42 cm² C、49 cm² D、63 cm²

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{16}$ =±4 B、 $3 \sqrt{2} - 2 \sqrt{2} = 1$ C、 $\sqrt{24} \div \sqrt{6} = 4$ D、 $\sqrt{\frac{2}{3}} \cdot \sqrt{6} = 2$

查看试题解析
4. 若代数式 $\frac{\sqrt{x}}{x - 1}$ 有意义，则实数x的取值范围是（）

A、x≠1 B、x≥0 C、x＞0 D、x≥0且x≠1

查看试题解析
5.
如图为某楼梯，测得楼梯的长为5米，高3米，计划在楼梯表面铺地毯，地毯的长度至少需要多米？（）

A、4 B、8 C、9 D、7

查看试题解析
6. 三角形的三边长分别为6，8，10，它的最短边上的高为（）

A、6 B、4.5 C、2.4 D、8

查看试题解析
7. 在平行四边形ABCD中，∠A：∠B：∠C：∠D的值可以是（）

A、1：2：3：4 B、1：2：2：1 C、1：2：1：2 D、1：1：2：2

查看试题解析
8. 菱形具有而矩形不一定具有的性质是（　　）

A、对角线互相垂直 B、对角线相等 C、对角线互相平分 D、对角互补

查看试题解析
9. 如图，过矩形ABCD的四个顶点作对角线AC、BD的平行线，分别相交于E、F、G、H四点，则四边形EFGH为（）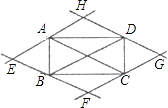

A、平行四边形 B、矩形 C、菱形 D、正方形

查看试题解析
10. △ABC中，AB=15，AC=13，高AD=12，则△ABC的周长为（　　）

A、42 B、32 C、42或32 D、37或33

查看试题解析
11. 如图，在矩形ABCD中，对角线AC，BD交于点O．已知∠AOB=60°，AC=16，则图中长度为8的线段有（）

A、2条 B、4条 C、5条 D、6条

查看试题解析
12. 如图，小聪在作线段AB的垂直平分线时，他是这样操作的：分别以A和B为圆心，大于 $\frac{1}{2}$ AB的长为半径画弧，两弧相交于C，D，则直线CD即为所求．根据他的作图方法可知四边形ADBC一定是（）

A、矩形 B、菱形 C、正方形 D、等腰梯形

查看试题解析
13. 已知一个菱形的周长是20cm，两条对角线的比是4：3，则这个菱形的面积是（）

A、12cm² B、24cm² C、48cm² D、96cm²

查看试题解析
14.
如图，正方形ABCD的边长为4，点E在对角线BD上，且∠BAE=22.5°，EF⊥AB，垂足为F，则EF的长为（　　）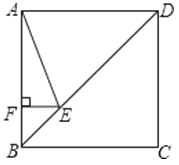

A、1 B、 $\sqrt{2}$ C、4﹣2 $\sqrt{2}$ D、3 $\sqrt{2}$ ﹣4

查看试题解析
15. 如图，在矩形ABCD中，点E，F分别在边AB，BC上，且AE= $\frac{1}{3}$ AB，将矩形沿直线EF折叠，点B恰好落在AD边上的点P处，连接BP交EF于点Q，对于下列结论：①EF=2BE；②PF=2PE；③FQ=4EQ；④△PBF是等边三角形．其中正确的是（）

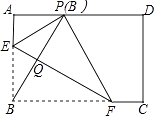A、①② B、②③ C、①③ D、①④

查看试题解析

二、解答题

16. 计算：
① $\sqrt{50} + \sqrt{18} - \sqrt{\frac{1}{2}}$ ．
②（3+ $\sqrt{3}$ ）（3﹣ $\sqrt{3}$ ）+ $\frac{\sqrt{8} + \sqrt{6}}{\sqrt{2}}$ ．

查看试题解析
17. 如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：

(1)、画线段AD∥BC且使AD=BC，连接CD；

(2)、线段AC的长为， CD的长为， AD的长为；

(3)、△ACD为三角形，四边形ABCD的面积为．

查看试题解析
18. 如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．

(1)、求证：∠ADB=∠CDB；

(2)、若∠ADC=90°，求证：四边形MPND是正方形．

查看试题解析
19. 如图，在正方形ABCD中，AD=2，E是AB的中点，将△BEC绕点B逆时针旋转90°后，点E落在CB的延长线上点F处，点C落在点A处．再将线段AF绕点F顺时针旋转90°得线段FG，连接EF，CG．

(1)、求证：EF∥CG；

(2)、求点C，点A在旋转过程中形成的 $\hat{A C}$ ， $\hat{A G}$ 与线段CG所围成的阴影部分的面积．

查看试题解析
20. 红安卷烟厂生产的“龙乡”牌香烟盒里，装满大小均匀的20支香烟，打开烟盒的顶盖后，二十支香烟排列成三行，经测量，一支香烟的直径约为0.75cm，长约为8.4cm．

(1)、试计算烟盒顶盖ABCD的面积（本小题计算结果不取近似值）．

(2)、制作这样一个烟盒至少需要多少面积的纸张（不计重叠粘合的部分，计算结果精确到0.1cm， $\sqrt{3}$ 取1.73）．

查看试题解析
21. 某校初中义务交于服务范围内学生人数持续增加，2012年学生数比2011年增加了a%，2013年学生数比2012年多了100人，这样2013年学生人数就比2011年增加了2a%．

(1)、求2012年学生人数比2011年多多少人？

(2)、由于教学楼改造，2013年的教室总面积比2011年增加了2.5a%，因而2013年每个学生人平均教室面积比2011年增加了 $\frac{1}{24}$ ，达到了 $\frac{1}{8}$ a（m²）．求该校2013年的教室总面积．

查看试题解析
22. 如图一，矩形ABCD中，AB=5cm，BC=4cm，E是BC上一点，将△CDE沿DE折叠，使点C落在AB上一点F处，连结DF、EF．

(1)、求BE的长度；

(2)、设点P、H、G分别在线段DE、BC、BA上，当BP=CP且四边形BGPH为矩形时，请说明矩形BGPH的长宽比为2：1，并求PE的长．（如图二）

查看试题解析
23. 如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．

(1)、求证：∠APB=∠BPH；

(2)、当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；

(3)、设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

查看试题解析