2016-2017学年江西省宜春市高安市九年级上学期期中数学试卷

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下列函数中不是二次函数的有（）

A、y=x（x﹣1） B、y= $\sqrt{2} x^{2}$ ﹣1 C、y=﹣x² D、y=（x+4）²﹣x²

查看试题解析
2. 将一元二次方程x²﹣2x﹣2=0配方后所得的方程是（）

A、（x﹣2）²=2 B、（x﹣1）²=2 C、（x﹣1）²=3 D、（x﹣2）²=3

查看试题解析
3. 如图，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 已知关于x的一元二次方程（a﹣1）x²+x+a²﹣1=0的一个根是0，则a的值为（）

A、1 B、﹣1 C、1或﹣1 D、 $\frac{1}{2}$

查看试题解析
5. 如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°至DE，连接AE，则△ADE的面积是（）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：
①b²＞4ac；②2a+b=0；③3a+c=0；④a+b+c=0．
其中正确结论的个数是（）

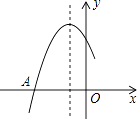A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

7. 抛物线y=a（x+1）（x﹣3）（a≠0）的对称轴是直线．

查看试题解析
8. 已知m，n是方程x²+4x﹣7=0的两根，则代数式 $\sqrt{m^{2} + n^{2} + 3 m n}$ 的值为．

查看试题解析
9. 已知x能使得 $\sqrt{x + 1}$ + $\sqrt{2 - x}$ 有意义，则点P（x+2，x﹣3）关于原点的对称点P′在第象限．

查看试题解析
10. 已知二次函数y=x²+bx+c经过点（3，0）和（4，0），则这个二次函数的解析式是．

查看试题解析
11. 若抛物线y=x²与直线y=x+2的交点坐标为（﹣1，1）和（2，4），则方程x²﹣x﹣2=0的解为．

查看试题解析
12. 如图，A（ $\sqrt{3}$ ，1），B（1， $\sqrt{3}$ ）．将△AOB绕点O旋转150°得到△A′OB′，则此时点A的对应点A′的坐标为．

查看试题解析

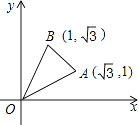
三、解答题

13. 用适当的方法解方程．

(1)、x²﹣3x+1=0

(2)、x（x﹣2）+2x﹣4=0．

查看试题解析
14. 如图，某小区在宽20m，长32m的矩形地面上修筑同样宽的人行道（图中阴影部分），余下的部分种上草坪．要使草坪的面积为540m² ，求道路的宽．

查看试题解析
15. 如图，有一座抛物线型拱桥，桥下面在正常水位AB时宽20米，水位上升3米就达到警戒线CD，这时水面宽度为10米．若洪水到来时，水位以每小时0.2米的速度上升从警戒线开始，再持续多少小时才能到拱桥顶？（平面直角坐标系是以桥顶点为点O的）

查看试题解析
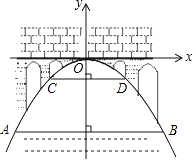16. 如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边（包括顶点）上，且四边形的顶点在方格的顶点上．

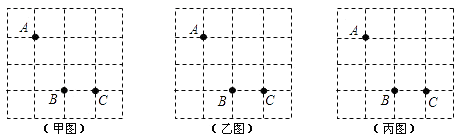(1)、在甲图中作出的四边形是中心对称图形但不是轴对称图形；

(2)、在乙图中作出的四边形是轴对称图形但不是中心对称图形；

(3)、在丙图中作出的四边形既是轴对称图形又是中心对称图形．

查看试题解析
17. 已知二次函数y=﹣ $\frac{1}{2}$ x²﹣x+ $\frac{7}{2}$

(1)、用配方法把该二次函数的解析式化为y=a（x+h）²+k的形式；

(2)、指出该二次函数图象的开口方向、顶点坐标和对称轴．

查看试题解析
18. 已知x₁ ， x₂是方程x²﹣4x+2=0的两根，求：

(1)、 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值；

(2)、（x₁﹣x₂）²的值．

查看试题解析
19. 如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（﹣3，2），B（0，4），C（0，2）．

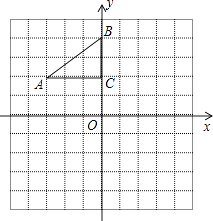(1)、将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A₁B₁C；平移△ABC，若点A的对应点A₂的坐标为（0，﹣4），画出平移后对应的△A₂B₂C₂；

(2)、若将△A₁B₁C绕某一点旋转可以得到△A₂B₂C₂；请直接写出旋转中心的坐标；

(3)、在x轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．

查看试题解析
20. 已知关于x的方程x²﹣（2k+1）x+4（k﹣ $\frac{1}{2}$ ）=0

(1)、求证：无论k取何值，这个方程总有实数根；

(2)、若等腰三角形ABC的一边长a=4，另两边b、c恰好是这个方程的两个根，求△ABC的周长．

查看试题解析
21. 小李按市场价格30元/千克收购了一批海鲜1000千克存放在冷库里，据预测，海鲜的市场价格将每天每千克上涨1元．冷冻存放这批海鲜每天需要支出各种费用合计310元，而且这些海鲜在冷库中最多存放160天，同时平均每天有3千克的海鲜变质．

(1)、设x天后每千克该海鲜的市场价格为y元，试写出y与x之间的函数关系式；

(2)、若存放x天后，将这批海鲜一次性出售．设这批海鲜的销售总额为P元，试写出P与x之间的函数关系式；

(3)、小李将这批海鲜存放多少天后出售可获得最大利润，最大利润是多少元？（利润W=销售总额﹣收购成本﹣各种费用）

查看试题解析
22. 在Rt△ABC中，∠ACB=90°，∠A=30°，点D是AB的中点，DE⊥BC，垂足为点E，连接CD．

(1)、如图1，DE与BC的数量关系是；

(2)、如图2，若P是线段CB上一动点（点P不与点B、C重合），连接DP，将线段DP绕点D逆时针旋转60°，得到线段DF，连接BF，请猜想DE、BF、BP三者之间的数量关系，并证明你的结论；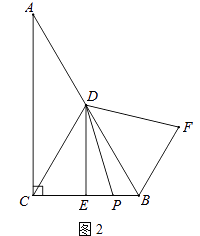

(3)、若点P是线段CB延长线上一动点，按照（2）中的作法，请在图3中补全图形，并直接写出DE、BF、BP三者之间的数量关系．

查看试题解析
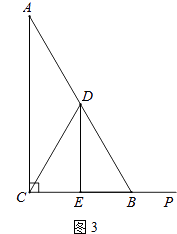23.
如图，在平面直角坐标系中，抛物线y=x²+mx+n经过点A（3，0）、B（0，﹣3），点P是直线AB上的动点，过点P作x轴的垂线交抛物线于点M，设点P的横坐标为t．

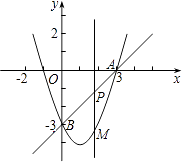(1)、分别求出直线AB和这条抛物线的解析式．

(2)、若点P在第四象限，连接AM、BM，当线段PM最长时，求△ABM的面积．

(3)、是否存在这样的点P，使得以点P、M、B、O为顶点的四边形为平行四边形？若存在，请求出点P的横坐标；若不存在，请说明理由．

查看试题解析