2016-2017学年江苏省苏州市吴江区九年级上学期期中数学试卷
试卷更新日期：2017-02-15 类型：期中考试
一、选择题
-
1. 下列方程中，一元二次方程有（ ）
①3x2+x=20；②2x2﹣3xy+4=0；③ ；④x2=1；⑤
A、2个 B、3个 C、4个 D、5个2. 若α、β是一元二次方程x2+2x﹣6=0的两根，则α+β=（ ）A、2 B、﹣2 C、3 D、﹣33. 关于x的一元二次方程（a﹣1）x2+x+a2﹣1=0的一个根是0，则a的值为（ ）A、1 B、﹣1 C、1或﹣1 D、4. （x2+y2）2﹣4（x2+y2）﹣5=0，则x2+y2的值为（ ）A、5 B、﹣1 C、5或﹣1 D、无法确定5. 某商品两次价格上调后，单位价格从4元变为4.84元，则平均每次调价的百分率是（ ）A、9% B、10% C、11% D、12%6. 如图，▱ABCD的一边AB为直径的⊙O过点C，若∠AOC=70°，则∠BAD等于（ ）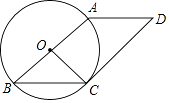
A、145° B、140° C、135° D、130°7. 如图，AB是⊙O的直径，弦CD⊥AB于点P，CD=10cm，AP：PB=1：5，那么⊙O的半径是（ ）
A、5 cm B、4 cm C、3 cm D、2 cm8. 等边三角形的内切圆半径、外接圆半径和一边上的高的比为（ ）A、1： ： B、1： ：2 C、1：2：3 D、1：2：9. 如图，过⊙O外一点P引⊙O的两条切线PA、PB，切点分别是A、B，OP交⊙O于点C，点D是优弧 上不与点A、点C重合的一个动点，连接AD、CD，若∠APB=80°，则∠ADC的度数是（ ）
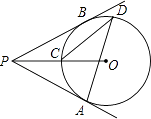A、15° B、20° C、25° D、30°10. 如图，以AB为直径的半圆绕A点，逆时针旋转60°，点B旋转到点B′的位置，已知AB=6，则图中阴影部分的面积为（ ）
A、6π B、5π C、4π D、3π二、填空题
-
11. 方程x2=3x的根是 ．12. 已知m，n是方程x2+2x﹣5=0的两个实数根，则m2+3mn+n2= ．13. 已知关于x的一元二次方程m2x2+（2m﹣1）x+1=0有两个不相等的实数根，则m的取值范围是 ．14. 甲、乙两同学解方程x2+px+q=0，甲看错了一次项系数，得根为2和7；乙看错了常数项，得根为1和﹣10，则原方程为 ．15. 已知⊙O的周长为12π，若点P到点O的距离为5，则点P在⊙O16. 已知3是关于x的方程x2﹣（m+1）x+2m=0的一个实数根，并且这个方程的两个实数根恰好是等腰△ABC的两条边的边长，则△ABC的周长为17. 如图，在⊙O的内接四边形ABCD中，∠A=70°，∠OBC=60°，则∠ODC= ．
18. 如图，点D为AC上一点，点O为边AB上一点，AD=DO．以O为圆心，OD长为半径作圆，交AC于另一点E，交AB于点F，G，连接EF．若∠BAC=22°，则∠EFG= ．
19. 如图，以原点O为圆心的圆交x轴于A、B两点，交y轴的正半轴于点C，D为第一象限内⊙O上的一点，若∠DAB=20°，则∠OCD=°．
20. 如图，海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形（弓形的弧是⊙O的一部分）区域内，∠AOB=80°．为了避免触礁，轮船P与A、B的张角∠APB的最大值为 ．
三、解答题
-
21. 解方程(1)、x2﹣6x﹣18=0（配方法）(2)、3（x﹣2）2=x（x﹣2）(3)、x2+2x﹣5=0(4)、（2x﹣3）2﹣2（2x﹣3）﹣3=0．22. 关于x的一元二次方程x2+2x﹣2m+1=0的两实数根之积为正，求实数m的取值范围？23. 已知关于x的一元二次方程x2﹣6x﹣k2=0（k为常数）．(1)、求证：方程有两个不相等的实数根；(2)、设x1 ， x2为方程的两个实数根，且x1+2x2=14，试求出方程的两个实数根和k的值．24. 某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件，每件获利40元．为了扩大销售，减少库存，增加利润，商场决定采取适当的降价措施，经过市场调查，发现如果每件童装每降价1元，则平均每天可多售出2件，要想平均每天在销售这种童装上获利1200元，那么每件童装应降价多少元？25. 某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，下图是水平放置的破裂管道有水部分的截面．
(1)、请你补全这个输水管道的圆形截面；(2)、若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．26. 如图，已知直线PA交⊙O于A、B两点，AE是⊙O的直径，点C为⊙O上一点，且AC平分∠PAE，过C作CD丄PA，垂足为D．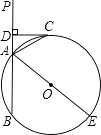
(1)、求证：CD为⊙O的切线；(2)、若DC+DA=6，⊙O的直径为10，求AB的长度．
