2016-2017学年甘肃省定西市临洮县九年级上学期期中数学试卷

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下面的图形中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 把方程x（x+2）=5（x﹣2）化成一般式，则a、b、c的值分别是（　　）

A、1，﹣3，10 B、1，7，﹣10 C、1，﹣5，12 D、1，3，2

查看试题解析
3. 将抛物线y=x²﹣4x﹣4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为（）

A、y=（x+1）²﹣13 B、y=（x﹣5）²﹣3 C、y=（x﹣5）²﹣13 D、y=（x+1）²﹣3

查看试题解析
4. 关于x的一元二次方程x²+ax﹣1=0的根的情况是（）

A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根

查看试题解析
5. 方程（x﹣1）（x+1）=1﹣x的解是（）

A、x=1 B、x=﹣1 C、x=1或x=﹣2 D、x=﹣1或 x=﹣2

查看试题解析
6. 进入夏季后，某电器商场为减少库存，对电热取暖器连续进行两次降价．若设平均每次降价的百分率是x，降价后的价格为y元，原价为a元，则y与x之间的函数关系式为（）

A、y=2a（x﹣1） B、y=2a（1﹣x） C、y=a（1﹣x²） D、y=a（1﹣x）²

查看试题解析
7. 若A（﹣4，y₁），B（﹣3，y₂），C（1，y₃）为二次函数y=x²+4x﹣5的图象上的三点，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
8. 如图，抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=1，与x轴的一个交点坐标为（﹣1，0），其部分图象如图所示，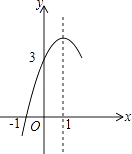
下列结论：
①4ac＜b²；
②方程ax²+bx+c=0的两个根是x₁=﹣1，x₂=3；
③3a+c＞0
④当y＞0时，x的取值范围是﹣1≤x＜3
⑤当x＜0时，y随x增大而增大
其中结论正确的个数是（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
9. 某市中心广场有各种音乐喷泉，其中一个喷水管喷水的最大高度为3米，此时距喷水管的水平距离为 $\frac{1}{2}$ 米，在如图所示的坐标系中，这个喷泉的函数关系式是（）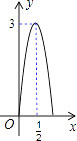

A、y=﹣（x﹣ $\frac{1}{2}$ ）²+3 B、y=﹣3（x+ $\frac{1}{2}$ ）²+3 C、y=﹣12（x﹣ $\frac{1}{2}$ ）²+3 D、y=﹣12（x+ $\frac{1}{2}$ ）²+3

查看试题解析
10. 把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′，边BC与D′C′交于点O，则四边形ABOD′的周长是（）

A、 $6 \sqrt{2}$ B、6 C、 $3 \sqrt{2}$ D、 $3 + 3 \sqrt{2}$

查看试题解析

二、填空题

11. 二次函数y=x²﹣4x﹣3的顶点坐标是（，）．

查看试题解析
12. 已知一元二次方程x²+mx+m﹣1=0有两个相等的实数根，则m= ．

查看试题解析
13. 如图，△OAB绕点O逆时针旋转80°到△OCD的位置，已知∠AOB=45°，则∠AOD等于度．

查看试题解析
14. 若将方程x²+6x=7化为（x+m）²=16，则m= ．

查看试题解析
15.
如图，在宽为20米、长为30米的矩形地面上修建两条同样宽的道路，余下部分作为耕地．若耕地面积需要551米² ，求修建的路宽．设路宽为xm，可列方程．

查看试题解析
16. 已知m是关于x的方程x²﹣2x﹣3=0的一个根，则2m²﹣4m= ．

查看试题解析
17. 已知抛物线y=ax²+bx+c（a≠0）的对称轴为直线x=1，且经过点P（3，0），则抛物线与x轴的另一个交点坐标为．

查看试题解析
18. 二次函数y=ax²+bx+c图象上部分点的对应值如下表：
x
﹣3
﹣2
﹣1
0
1
2
3
4
y
6
0
﹣4
﹣6
﹣6
﹣4
0
6
则使y＜0的x的取值范围为．

查看试题解析

三、解答题

19. 按要求解一元二次方程：

(1)、x²﹣10x+9=0（配方法）

(2)、x（x﹣2）+x﹣2=0（因式分解法）

查看试题解析
20. 选择适当的方法解方程：

(1)、2（x﹣3）=3x（x﹣3）．

(2)、2x²﹣3x+1=0．

查看试题解析
21. 正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：

(1)、作出△ABC绕点A逆时针旋转90°的△AB₁C₁ ，再作出△AB₁C₁关于原点O成中心对称的△A₁B₂C₂ ．

(2)、点B₁的坐标为，点C₂的坐标为．

查看试题解析
22. 已知二次函数的图象以A（﹣1，4）为顶点，且过点B（2，﹣5）．

(1)、求该二次函数的表达式；

(2)、求该二次函数图象与y轴的交点坐标．

查看试题解析
23. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m²？

查看试题解析

四、解答题

24. 已知二次函数y=x²﹣2x﹣3．

(1)、用配方法将解析式化为y=（x﹣h）²+k的形式；

(2)、求这个函数图象与x轴的交点坐标．

查看试题解析
25. 已知关于x的方程mx²+x+1=0，试按要求解答下列问题：

(1)、当该方程有一根为1时，试确定m的值；

(2)、当该方程有两个不相等的实数根时，试确定m的取值范围．

查看试题解析
26. 如图，已知抛物线y=x²+bx+c经过A（﹣1，0）、B（3，0）两点．

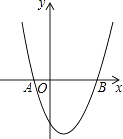(1)、求抛物线的解析式和顶点坐标；

(2)、当0＜x＜3时，求y的取值范围；

(3)、点P为抛物线上一点，若S_△_PAB=10，求出此时点P的坐标．

查看试题解析
27. 阅读新知：移项且合并同类项之后，只含有偶次项的四次方程称作双二次方程．其一般形式为ax⁴+bx²+c=0（a≠0），一般通过换元法解之，具体解法是设 x²=y，则原四次方程化为一元二次方程：ay²+by+c=0，解出y之后代入x²=y，从而求出x的值．例如解：4x⁴﹣8y²+3=0
解：设x²=y，则原方程可化为：4y²﹣8y+3=0
∵a=4，b=﹣8，c=3
∴b²﹣4ac=﹣（﹣8）²﹣4×4×3=16＞0
∴y= $\frac{- (- 8) \pm \sqrt{16}}{2 \times 4}$ = $\frac{8 \pm 4}{8}$
∴y₁= $\frac{1}{2}$ ，
∴y₂= $\frac{3}{2}$
∴当y₁= $\frac{1}{2}$ 时，x²= $\frac{1}{2}$
∴x₁= $\frac{\sqrt{2}}{2}$ ，x₂=﹣ $\frac{\sqrt{2}}{2}$ ；当y₁= $\frac{3}{2}$ 时，x²= $\frac{3}{2}$
∴x₃= $\frac{\sqrt{6}}{2}$ ，x₄=﹣ $\frac{\sqrt{6}}{2}$
小试牛刀：请你解双二次方程：x⁴﹣2x²﹣8=0
归纳提高：思考以上解题方法，试判断双二次方程的根的情况，下列说法正确的是（选出所有的正确答案）
①当b²﹣4ac≥0时，原方程一定有实数根；②当b²﹣4ac＜0时，原方程一定没有实数根；③当b²﹣4ac≥0，并且换元之后的一元二次方程有两个正实数根时，原方程有4个实数根，换元之后的一元二次方程有一个正实数根一个负实数根时，原方程有2个实数根；④原方程无实数根时，一定有b²﹣4ac＜0．

查看试题解析
28.
如图，平面直角坐标系xOy中，直线AC分别交坐标轴于A，C（8，0）两点，AB∥x轴，B（6，4）．

(1)、求过B，C两点的抛物线y=ax²+bx+4的表达式；

(2)、点P从C点出发以每秒1个单位的速度沿线段CO向O点运动，同时点Q从A点出发以相同的速度沿线段AB向B点运动，其中一个动点到达端点时，另一个也随之停止运动．设运动时间为t秒．当t为何值时，四边形BCPQ为平行四边形；

(3)、若点M为直线AC上方的抛物线上一动点，当点M运动到什么位置时，△AMC的面积最大？求出此时M点的坐标和△AMC的最大面积．

查看试题解析

x	﹣3	﹣2	﹣1	0	1	2	3	4
y	6	0	﹣4	﹣6	﹣6	﹣4	0	6