2016-2017学年山东省泰安市泰山区八年级上学期期中数学试卷（五四学制）

试卷更新日期：2017-02-15 类型：期中考试

进入出卷网下载

一、选择题

1. 下列等式从左到右的变形中，属于因式分解的是（）

A、a（b﹣5）=ab﹣5a B、a²﹣4a+4=a（a﹣4）+4 C、x²﹣81y²=（x+9y）（x﹣9y） D、（3x﹣2）（2x+1）=6x²﹣x﹣2

查看试题解析
2. 下列分式中，属于最简分式的是（）

A、 $\frac{4}{2 x}$ B、 $\frac{2 x}{x^{2} + 1}$ C、 $\frac{x - 1}{x^{2} - 1}$ D、 $\frac{1 - x}{x - 1}$

查看试题解析
3. 在一次“爱心互助”捐款活动中，某班第一小组8名同学捐款的金额（单位：元）如下表所示：
金额/元
5
6
7
10
人数
2
3
2
1
这8名同学捐款的平均金额为（　　）

A、3.5元 B、6元 C、6.5元 D、7元

查看试题解析
4. 多项式m²﹣4n²与m²﹣4mn+4n²的公因式是（　　）

A、（m+2n）（m﹣2n） B、m+2n C、m﹣2n D、（m+2n）（m﹣2n）²

查看试题解析
5. 甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是S_甲²=0.65，S_乙²=0.55，S_丙²=0.50，S_丁²=0.45，则射箭成绩最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
6. 若分式 $\frac{x^{2} - 4}{x + 2}$ 的值为0，则（）

A、x=2 B、x=±2 C、x=﹣2 D、x=0

查看试题解析
7. 下列因式分解正确的是（）

A、4a²﹣4a+1=4a（a﹣1）+1 B、x²﹣4y²=（x+4y）（x﹣4y） C、 $\frac{9}{4}$ x²﹣x+ $\frac{1}{9}$ =（ $\frac{3}{2}$ x﹣ $\frac{1}{3}$ ）² D、2xy﹣x²﹣y²=﹣（x+y）²

查看试题解析
8. 下列多项式：①x²+y²；②x²﹣1；③x³+4x﹣4；④x²﹣10x+25，其中能直接用公式法因式分解的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 八年级一班与二班的同学在一次数学测验中的成绩统计情况如下表：
班级
参加人数
中位数
平均数
方差
一
49
84
80
186
二
49
85
80
161
某同学分析后得到如下结论：
①一班与二班学生平均成绩相同；
②二班优生人数多于一班（优生线85分）；
③一班学生的成绩相对稳定．
其中正确的是（）

A、①② B、①③ C、①②③ D、②③

查看试题解析
10. 化简 $\frac{a + 1}{a^{2} - 2 a + 1}$ ÷（1+ $\frac{2}{a - 1}$ ）的结果是（）

A、 $\frac{1}{a - 1}$ B、 $\frac{1}{a + 1}$ C、 $\frac{1}{a^{2} - 1}$ D、 $\frac{1}{a^{2} + 1}$

查看试题解析
11. 若把分式 $\frac{x + y}{2 x y}$ 中的x和y都变为原来的3倍，那么分式的值变为原来的（）

A、 $\frac{1}{3}$ 倍 B、3倍 C、不变 D、 $\frac{1}{6}$ 倍

查看试题解析
12. 满足方程 $\frac{1}{x - 2} + 3 = \frac{x - 1}{x - 2}$ 的x的值是（）

A、x=2 B、x=﹣2 C、x=0 D、无解

查看试题解析
13. 若a+b+1=0，则3a²+3b²+6ab的值是（）

A、3 B、﹣3 C、1 D、﹣1

查看试题解析
14. 为响应承办“绿色奥运”的号召，九年级（1）班全体师生义务植树300棵．原计划每小时植树x棵，但由于参加植树的全体师生植树的积极性高涨，实际工作效率提高为原计划的1.2倍，结果提前20分钟完成任务．则下面所列方程中，正确的是（）

A、 $\frac{300}{x} - \frac{20}{60} = \frac{300}{1.2 x}$ B、 $\frac{300}{x} - \frac{300}{1.2 x} = 20$ C、 $\frac{300}{x} - \frac{300}{x + 1.2 x} = \frac{20}{60}$ D、 $\frac{300}{x} = \frac{300}{1.2 x} - \frac{20}{60}$

查看试题解析

二、填空题

15. 因式分解：m²+4m+4= ．

查看试题解析
16. 分式 $\frac{1}{x^{2} - 3 x}$ 与 $\frac{2}{9 - x^{2}}$ 的最简公分母是．

查看试题解析
17.
某班全体学生参加了一次“献爱心一日捐”活动，捐款人数与捐款额如图所示，根据图中所提供的信息，你认为这次捐款活动中捐款额的中位数是元．

查看试题解析
18. 一组数据按从小到大的顺序排列为1，2，3，x，4，5，若这组数据的平均数为3，则x的值是．

查看试题解析
19. 若4x²+mx+9是一个完全平方式，则实数m的值是．

查看试题解析
20. 若分式方程 $\frac{m}{x^{2} - 4}$ ﹣ $\frac{2}{x + 2}$ = $\frac{1}{x - 2}$ 有增根，则m的值是．

查看试题解析
21. 已知a²﹣3ab+b²=0（a≠0，b≠0），则代数式 $\frac{b}{a}$ + $\frac{a}{b}$ 的值等于．

查看试题解析
22. 一艘轮船在静水中的最大航速为30千米/时，它沿江以最大航速顺流航行100千米所用的时间与以最大航速逆流航行60千米所用的时间相等，问：江水的流速为多少？设江水的流速为x千米/时，则可列方程为．

查看试题解析

三、解答题

23. 因式分解

(1)、4m（a﹣b）﹣6n（b﹣a）；

(2)、16（m﹣n）²﹣9（m+n）² ．

查看试题解析
24. 计算

(1)、 $\frac{a^{2} - 1}{a^{2} + 4 a + 4}$ ÷ $\frac{a + 1}{a + 2}$ ；

(2)、 $\frac{a}{a^{2} - 1}$ + $\frac{3 a + 1}{a^{2} - 1}$ + $\frac{2 a + 3}{1 - a^{2}}$ ；

(3)、 $\frac{4}{x^{2} - 4}$ + $\frac{2}{x + 2}$ ﹣ $\frac{1}{x - 2}$ ．

查看试题解析
25. 先化简，再求值： $(a - 3 - \frac{7}{a + 3}) \div \frac{a - 4}{2 a + 6}$ ，其中a=﹣1．

查看试题解析
26. 解方程

(1)、 $\frac{2}{x - 3} = \frac{3}{2 x - 1}$ ；

(2)、 $\frac{1}{x + 1} + \frac{2}{x - 1} = \frac{4}{x^{2} - 1}$ ．

查看试题解析
27. 为了解某校学生的身高情况，随机抽取该校男生、女生进行抽样调查．已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
身高情况分组表（单位：cm）
组别
身高
A
x＜155
B
155≤x＜160
C
160≤x＜165
D
165≤x＜170
E
x≥170
根据图表提供的信息，回答下列问题：

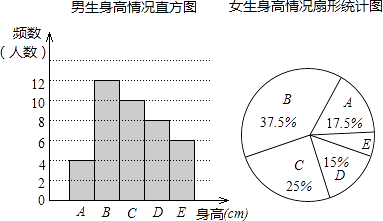(1)、样本中，男生的身高众数在组，中位数在组；

(2)、样本中，女生身高在E组的人数有人；

(3)、已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？

查看试题解析
28. 某文化用品商店用2000元购进一批学生书包，面市后发现供不应求，商店又购进第二批同样的书包，所购数量是第一批购进数量的3倍，但单价贵了4元，结果第二批用了6300元．

(1)、求第一批购进书包的单价是多少元？

(2)、若商店销售这两批书包时，每个售价都是120元，全部售出后，商店共盈利多少元？

查看试题解析

班级	参加人数	中位数	平均数	方差
一	49	84	80	186
二	49	85	80	161

组别	身高
A	x＜155
B	155≤x＜160
C	160≤x＜165
D	165≤x＜170
E	x≥170

金额/元	5	6	7	10
人数	2	3	2	1